Backtracking – N Queens Problem – Better Solution

Objective : In chess, a queen can move as far as she pleases, horizontally, vertically, or diagonally. A chess board has 8 rows and 8 columns. The standard 8 by 8 Queen’s problem asks how to place 8 queens on an ordinary chess board so that none of them can hit any other in one move.(Source: http://www.math.utah.edu/~alfeld/queens/queens.html)

Here we are solving it for N queens in NxN chess board.

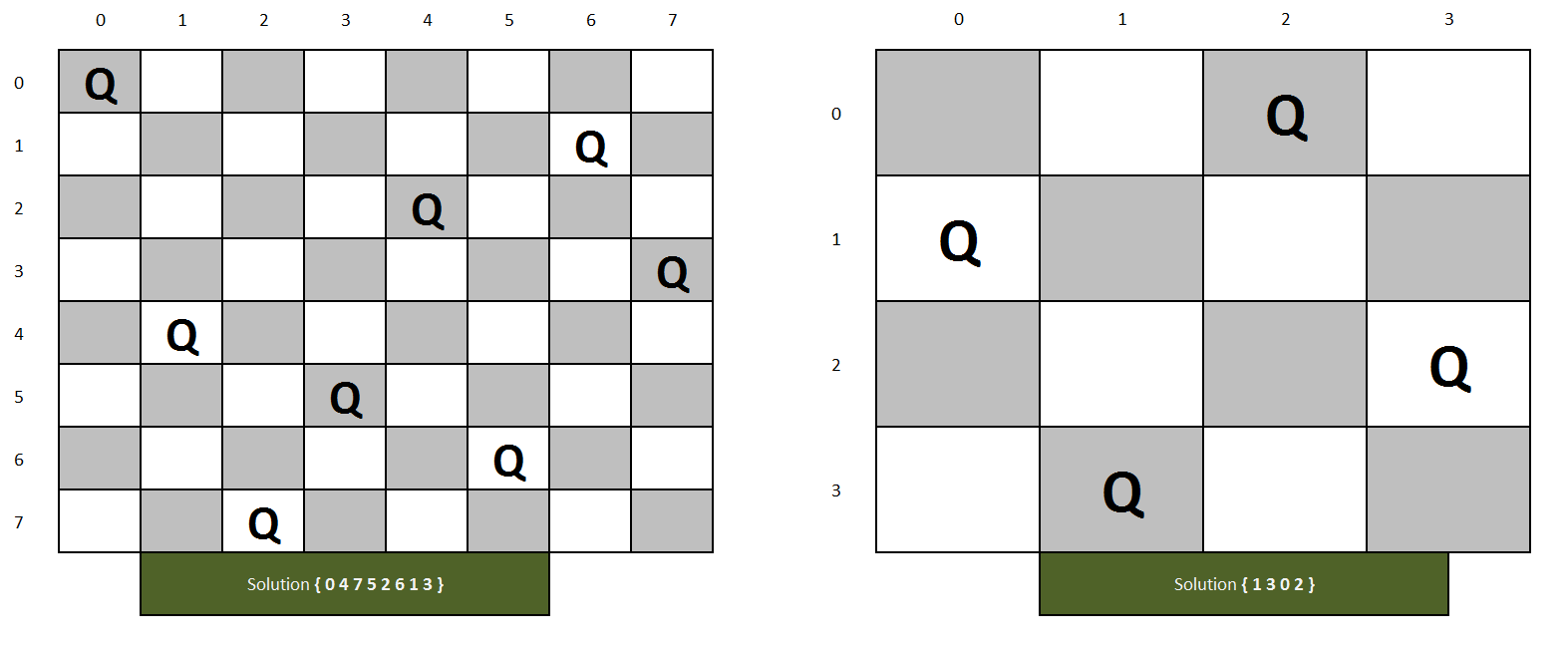
Approach:

This earlier approach we have seen solution matrix, at every row we have only one entry as 1 and rest of the entries are 0. Solution matrix takes O(N²) space. We can reduce it to O(N). We will solve it by taking one dimensional array and consider solution[1] = 2 as “Queen at 1st row is placed at 2nd column.

result[i]=j means queen at i-th row is placed at j-th column.

Check if Queens placed at (x1, y1) and (x2,y2) are safe

• x1==x2 means same rows,
• y1==y2 means same columns
• |x2-x1|==|y2-y1| means they are placed in diagonals.

Code: Run This Code

Run This Code

Output:	
Order of 6 queens[1, 3, 5, 0, 2, 4]
Order of 6 queens[2, 5, 1, 4, 0, 3]
Order of 6 queens[3, 0, 4, 1, 5, 2]
Order of 6 queens[4, 2, 0, 5, 3, 1]

Reference :”https://www.youtube.com/watch?v=p4_QnaTIxkQ”