Construct a binary tree from given Inorder and Level Order Traversal

Objective: – Given a inorder and level order traversal, construct a binary tree from that.

Input: Inorder and level order traversal

Approach:

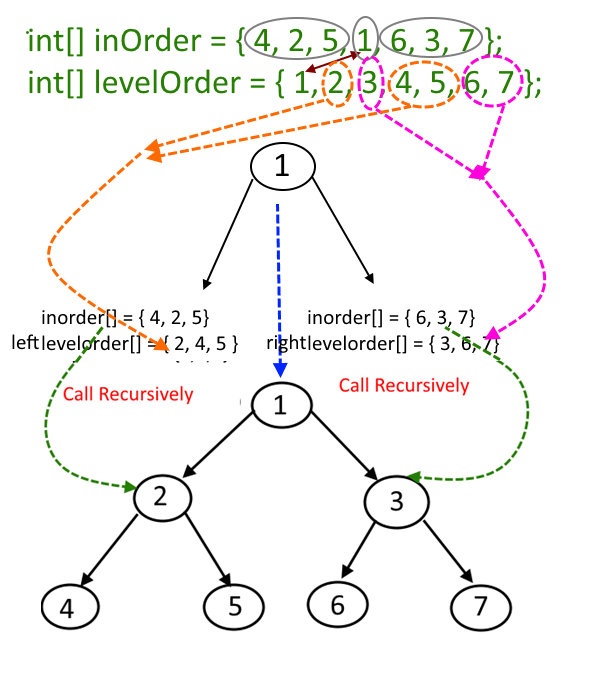
int[] inOrder = { 4, 2, 5, 1, 6, 3, 7 };
int[] levelOrder = { 1, 2, 3, 4, 5, 6, 7 };

• First element in the levelorder [] will be the root of the tree, here it is 1.
• Now the search ele­ment 1 in inorder[], say you find it at posi­tion i, once you find it, make note of ele­ments which are left to i (this will con­struct the left­sub­tree) and ele­ments which are right to i ( this will con­struct the rightSubtree).
• Suppose in previous step, there are X number of elements which are left of ‘i’ (which will construct the leftsubtree), but these X elements will not be in the consecutive in levelorder[] so we will extract these elements from levelorder[] by maintaining their sequence and store it in an array say newLeftLevel[].
• Similarly if there are Y number of elements which are right of ‘i’ (which will construct the rightsubtree), but these Y elements will not be in the consecutive in levelorder[] so we will extract these elements from levelorder[] by maintaining their sequence and store it in an array say newRightLevel[].
• From previous two steps construct the left and right subtree and link it to root.left and root.right respectively by making recursive calls using newLeftLevel[] and newRightLevel[].
• See the picture for better explanation.

Complete Code:Run This Code

Run This Code
Output:

inorder traversal of constructed tree : 
  4  2  5  1  6  3  7