|
This post is completed by 3 users
|
Add to List |
134. Diameter Of a Binary Tree
Objective: - Given a binary tree, write an algorithm to find the tree's diameter.
What is the Diameter Of a Tree: The tree's diameter is defined as The longest path or route between any two nodes in a tree. The path may or may not go through the root.
Example:
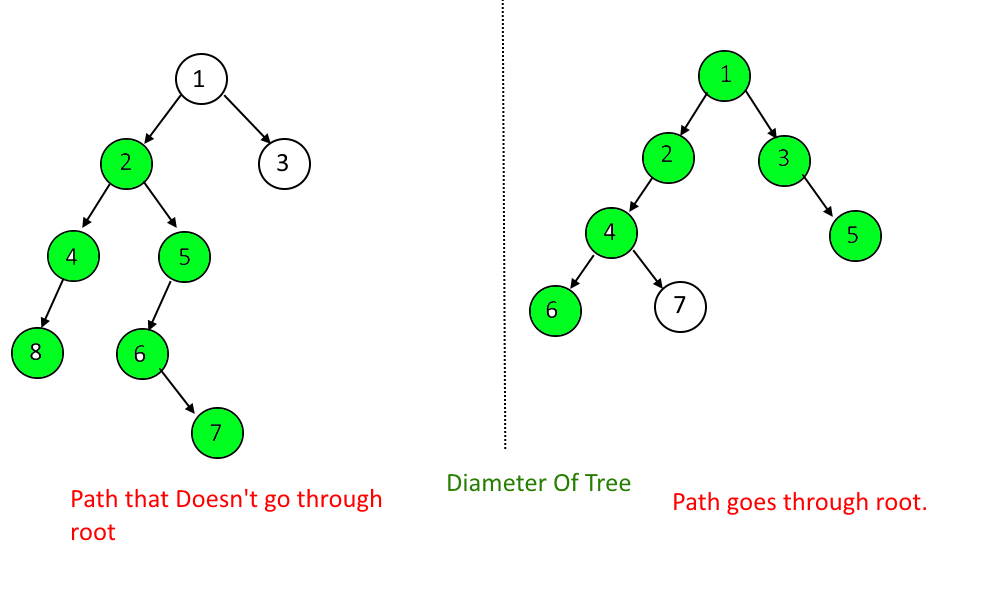
Approach:
The diameter of a tree w.r.t root can be defined as
Maximum(Diameter of left subtree, Diameter of right subtree, Longest path between two nodes which passes through the root.)
Now the diameter of left and right subtrees can be solved recursively. The longest path between two nodes that passes through the root can be calculated as 1 + height of the left subtree + height of the right subtree.
Please read this post to learn how to find a tree's height.
We will explain Two approaches, The First one will be the Naive approach -O(N2) and then we will improve it to O(N).
Naive Approach:
- Find the height of the left subtree.
- Find the height of the right subtree.
- Find the left diameter.
- Find the right diameter.
- Return the Maximum(Diameter of the left subtree, the Diameter of the right subtree, and the Longest path between two nodes that passes through the root.)
Time Complexity: When calculating the diameter, every iteration for every node, is calculating the height of the tree separately in which we iterate the tree from top to bottom, and when we calculate diameter recursively so it is O(N2)
Output: Diameter of Tree: 6
Now we will improve it further. If you notice at every node to find the diameter we are calling a separate function to find the height. We can improve it by finding the height of the tree and diameter in the same iteration.
Approach:
Every node will return the two pieces of information in the same iteration: the node's height and the tree's diameter with respect to that node. Look at the code below
Output: Diameter of Tree 6

