|
This post is completed by 2 users
|
Add to List |
207. Dynamic Programming - Count all paths from top left to bottom right of a mXn matrix
Objective: Given a two-dimensional matrix, write an algorithm to count all possible paths from the top left corner to the bottom-right corner. You are allowed to move only in two directions, move right OR move down.
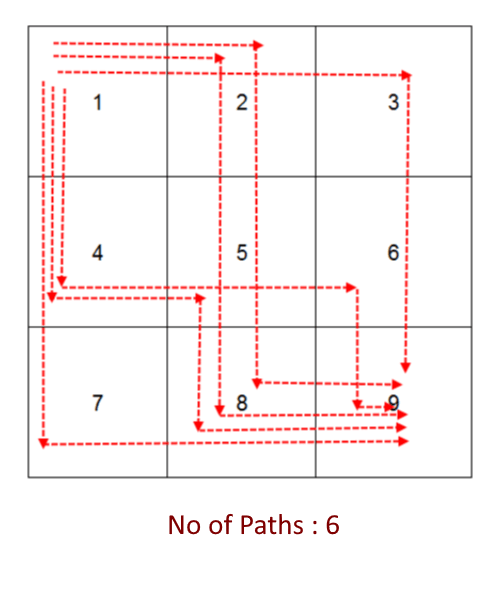
Example:
Approach:
Recursion- Earlier we have seen "Print All Paths from Top left to bottom right in Two Dimensional Array". The current problem is the subset of that problem. Here we will just count the number of paths, and will not print them.
From every cell, you will have two options to make a move, either to go right OR down. The base case will check if you have reached either the last row OR the last column then there is only one way to reach the last cell to travel through that row or column. x
Recursive Code:
Time Complexity: It will be exponential since we are solving many sub-problems repeatedly. We will use the Bottom-up approach of Dynamic programming and store the results of sub-problems to reuse them in the future.
Output:
No Of Path (Recursion):- 6 No Of Path (DP):- 6

