|
This post is completed by 2 users
|
Add to List |
208. Dynamic Programming - Count all paths in 2D Matrix with Obstructions in it
Objective: Given a two-dimensional matrix, write an algorithm to count all possible paths from the top left corner to the bottom-right corner. You are allowed to move only in two directions, move right OR move down. There are few obstructions as well, which means few cells are blocked and you cannot travel that cell.
Many times this problem is referred to as the "Robot Travel Problem". Given a 2d matrix, how many ways a robot can travel from the top left corner to the bottom right corner and there are few cells in which the robot cannot travel?
Example:
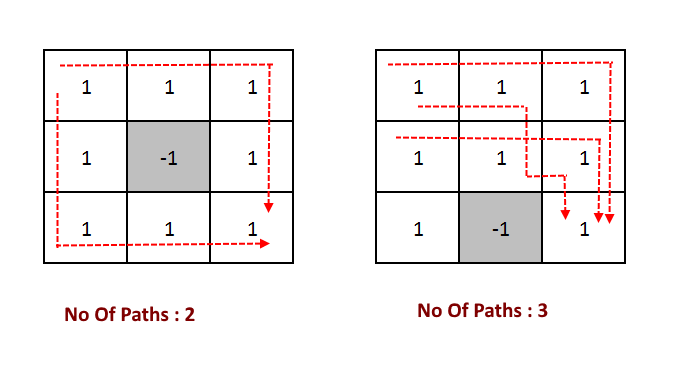
Approach:
- This problem is the extension of the problem "Count all paths from top left to bottom right of a mXn matrix".
- All we need to take care of is one extra condition we cannot travel to the blocked cells.
- In the recursive solution given in "Count all paths from top left to the bottom right of a mXn matrix" just check for the condition if the cell is not blocked.
- In a Dynamic programming solution, we need to take care of two conditions, first, we are not solving it for blocked cells, and solving for other cells does not involve blocked cells.
- See the code for a better understanding.
Output:
No Of Path (Recursion):- 1 No Of Path (DP):- 1

