Dynamic Programming – Longest Common Subsequence
Objective: Given two string sequences, write an algorithm to find the length of longest subsequence present in both of them.
These kind of dynamic programming questions are very famous in the interviews like Amazon, Microsoft, Oracle and many more.
What is Longest Common Subsequence: A longest subsequence is a sequence that appears in the same relative order, but not necessarily contiguous(not substring) in both the string.
Example:
String A = "acbaed";
String B = "abcadf";
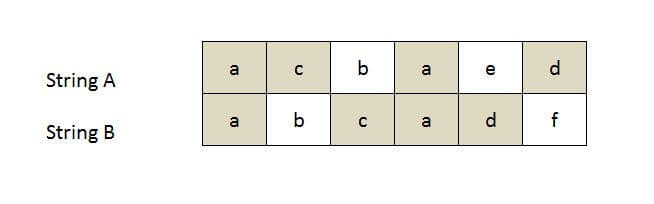
Longest Common Subsequence(LCS): acad, Length: 4
Approach:
Recursion:
Start comparing strings in reverse order one character at a time.
Now we have 2 cases –
- Both characters are same
- add 1 to the result and remove the last character from both the strings and make recursive call to the modified strings.
- Both characters are different
- Remove the last character of String 1 and make a recursive call and remove the last character from String 2 and make a recursive and then return the max from returns of both recursive calls. see example below
Example:
Case 1:
String A: "ABCD", String B: "AEBD"
LCS("ABCD", "AEBD") = 1 + LCS("ABC", "AEB")
Case 2:
String A: "ABCDE", String B: "AEBDF"
LCS("ABCDE", "AEBDF") = Max(LCS("ABCDE", "AEBD"), LCS("ABCD", "AEBDF"))
Code:
Output:
LCS :4
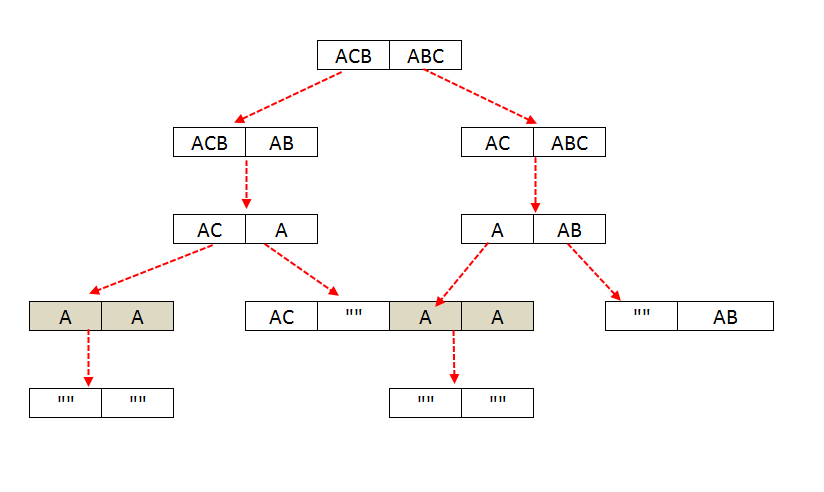
In a given string of length n, there can be 2n subsequences can be made, so if we do it by recursion then Time complexity will O(2n) since we will solving sub problems repeatedly.
Dynamic Programming:
We will solve it in Bottom-Up and store the solution of the sub problems in a solution array and use it when ever needed, This technique is called Memoization. See the code for better explanation.
Code:
Output:
LCS :4
Print the Longest Common Subsequence:
Take a look into the LCS[][] used in the code
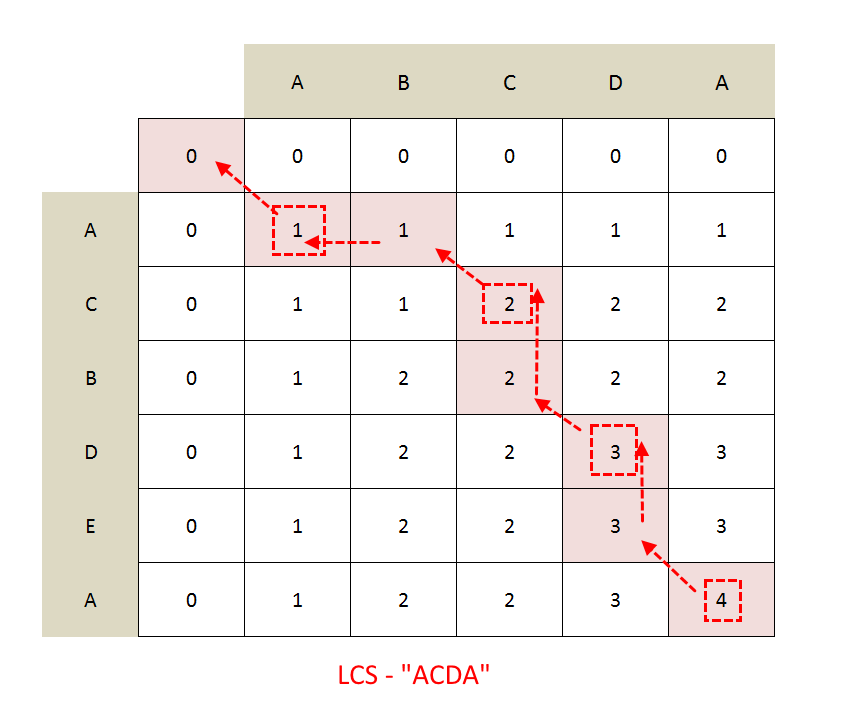
Start from bottom right corner and track the path and mark the cell from which cell the value is coming and whenever you go diagonal ( means last character of both string has matched, so we reduce the length of both the strings by 1, so we moved diagonally), mark those cells, this is our answer.
Complete Code( Include Printing Result):
Output:
ACDA 0 0 0 0 0 0 0 1 1 1 1 1 0 1 1 2 2 2 0 1 2 2 2 2 0 1 2 2 3 3 0 1 2 2 3 3 0 1 2 2 3 4 LCS :4
Click here to see the code for Dynamic Programming – Top Down Approach:
Is it a typo in case 2 of the example?
Yes , corrected it , Thanks Le
In case 1 using recursive function, can it be extended to print LCS as well?
What is the similarity between 85.17.19.4.
2
How and why is your solution top-down approach? You started at zero and reached the solution step by step. Is it bottom-top approach?
For beginner,you can check also below naive and simple logic
public class LCSNaive {
public static void main(String[] args) {
String str1 = “ACBDEA”;
String str2 = “ABCDA”;
String result = lcs(str1, str2);
System.out.println(result);
}
static String lcs(String str1, String str2) {
int len1 = str1.length();
int len2 = str2.length();
int j = 0, ji = 0;
String result = “”;
for (int i = 0; i < len1; i++) {
for (; j < len2; j++) {
if (str1.charAt(i) == str2.charAt(j)) {
result += str1.charAt(i);
ji = j;
break;
}
}
if (j == len2)
j = ji + 1;
}
return result;
}
}
It’s not working with big string.
Thank you so much for the article 🙂
Hi SJ, looks like in “find” method we could skip two “for” cycles which set 0 into LCS array, because they are constructed with 0 values. Also, “String[][] solution” variable purpose is not clear in that method, we could just omit it and result will be the same.
it’s bottom up approach ..
Studying the solution for DP it is bottom approach, please fix the typo