|
This post is completed by 2 users
|
Add to List |
160. Dynamic Programming - Longest Increasing Subsequence
Objective: The longest Increasing Subsequence (LIS) problem is to find the length of the longest subsequence in a given array such that all elements of the subsequence are sorted in increasing order.
Example:
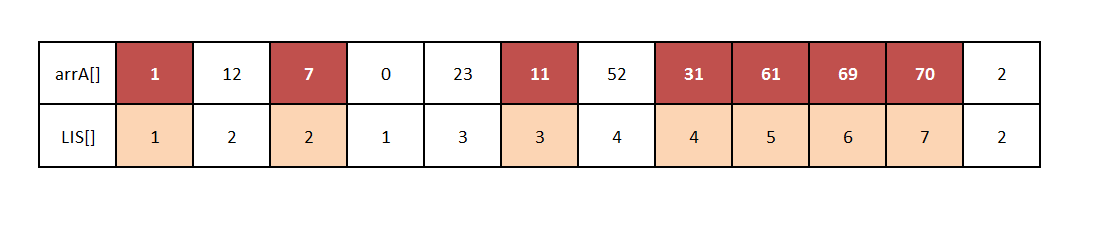
int [] A = { 1, 12, 7, 0, 23, 11, 52, 31, 61, 69, 70, 2 };
length of LIS is 7 and LIS is {1, 12, 23, 52, 61, 69, 70}.
Approach:
Optimal Substructure:
LIS(i) - Length of longest increasing subsequence which includes element A[i] as its last element.
LIS(i) = 1 + Max j=1 to i-1 {LIS(j)} if A[i]>A[j] for 1<j</j
Overlapping Subproblems:
If we solve using recursion for calculating the solution for jth index we will be solving the subproblems again which we had solved earlier while solving the solution for (j-1)th index.
Example:
A[] = {3, 4, 1, 5}
i=1 , LIS(1) = 1
i=2 , LIS(2) = 1+ Max(LIS(1)) = 1 +1 =2 (4>3)
i=3 , LIS(3) = 1 (1<3, 1<4)
i=4 , LIS(4) = 1+ Max(LIS(1),LIS(2), LIS(3))
= 1 + Max(1,2,1) = 3
Output:
Output: Longest Increasing subsequence: 7 Actual Elements: 1 7 11 31 61 69 70
NOTE: To print the Actual elements -
- find the index which contains the longest sequence, print that index from main array.
- Start moving backwards and pick all the indexes which are in sequence (descending).
- If longest sequence for more than one indexes, pick any one.
From our code LIS[] =