|
This post is completed by 2 users
|
Add to List |
174. Dynamic Programming - Maximum Product Cutting Problem
Objective: Given a rope of length n meters, write an algorithm to cut the rope in such a way that the product of different lengths of rope is maximum. At least one cut has to be made.
Note: Assume that the length of the rope is more than 2 meters since at least one cut has to be made.
This is yet another problem where you will see the advantage of dynamic programming over recursion. I will show you how storing and reusing the results of sub-problems will reduce the complexity of an algorithm significantly. This kind of questions is asked in interviews like Amazon, Microsoft, Google, etc.
Example:
• Rope length: 2 • Options: (1*1) • Maximum Product Cutting : 1*1 = 1 • Rope length: 3 • Options: (1*1*1, 2*1) • Maximum Product Cutting : 2*1 = 2 • Rope length: 4 • Options: (1*1*1*1, 2*1*1, 3*1, 2*2) • Maximum Product Cutting : 2*2 = 4 • Rope length: 5 • Options: (1*1*1*1*1, 2*1*1*1, 3*1*1, 2*2*1, 3*2) • Maximum Product Cutting : 3*2 = 6
Approach:
Using Recursion:
This problem is similar to the "Rod Cutting Problem".
- Check the products of all possible cuts that can be made in the rope and return the maximum product.
- For every length, there are two options, either a cut to be made or not. Solve the problem for both options and choose the maximum.
- After Making the cut the further options are, Either this cut will produce the max product OR we need to make further cuts
Recursive Equation:
Let MPC(n) is the maximum product for length n.
- MPC(n) = max(i*(n-i), i*MPC(n-i)) for all (i=1,2.....n) (After Making the cut the further options are , Either this cut will produce the max product OR we need to make further cuts).
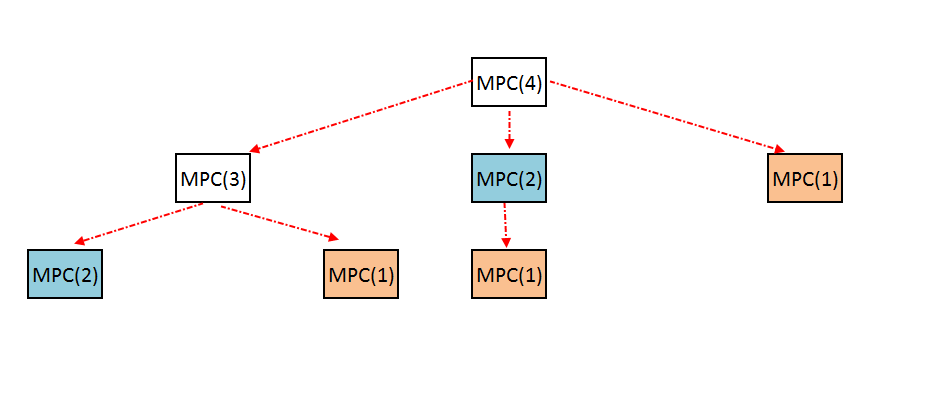
Time Complexity: O(2n).
But yet again we are solving many sub-problems repeatedly.
Dynamic Programming:
We will solve this problem in a Bottom-Up manner.
We will store the solutions for sub-problems when it getting solved for the first time and use them again in the future so that we don't have to solve them again.
Time Complexity: O(N^2)
See the Code for a better understanding.
Output: Dynamic Programming: Maximum product cutting in 10 is: 36

