Dynamic Programming – Maximum Subarray Problem
Objective: The maximum subarray problem is the task of finding the contiguous subarray within a one-dimensional array of numbers which has the largest sum.
Example:
int [] A = {−2, 1, −3, 4, −1, 2, 1, −5, 4};
Output: contiguous subarray with the largest sum is 4, −1, 2, 1, with sum 6.
Approach:
Earlier we have seen how to solve this problem using Kadane’s Algorithm. In this post we will how to solve it using Dynamic programming.
We will solve this problem in bottom-up manner.
let’s say
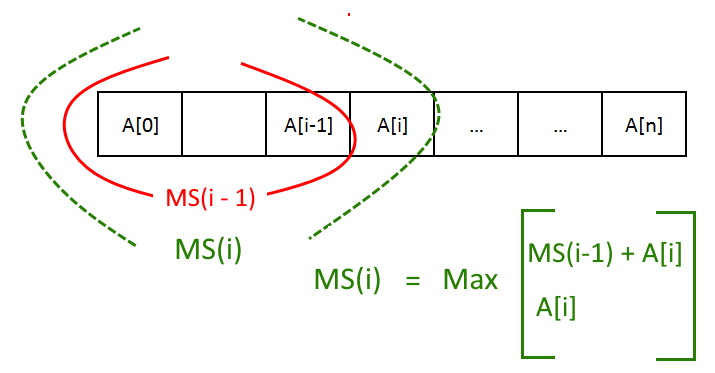
“MS(i) is maximum sum ending at index i”
To calculate the solution for any element at index “i” has two options
- EITHER added to the solution found till “i-1“th index
- OR start a new sum from the index “i“.
Recursive Solution:
MS(i) = Max[MS(i-1) + A[i] , A[i]]
Complete Code:
Output:
[0, 1, 3, 0, 0, 2, 9, 7, 10] Maximum subarray is 10
