Dynamic Programming – Rod Cutting Problem

Objective: Given a rod of length n inches and a table of prices p_i, i=1,2,…,n, write an algorithm to find the maximum revenue r_n obtainable by cutting up the rod and selling the pieces.

This is a very good basic problem after Fibonacci sequence if you are new to Dynamic programming. We will see how dynamic programming is used to overcome the issues with recursion(Time Complexity).

Given: Rod lengths are integers and For i=1,2,…,n we know the price p_i of a rod of length i inches

Example:

Length	1	2	3	4	5	6	7	8	9	10
Price	1	5	8	9	10	17	17	20	24	30

for rod of length: 4
Ways to sell :
•	selling length : 4  ( no cuts) , Price: 9
•	selling length : 1,1,1,1  ( 3 cuts) , Price: 4
•	selling length : 1,1,2  ( 2 cuts) , Price: 7
•	selling length : 2,2  ( 1 cut) , Price: 10
•	selling length : 3, 1  ( 1 cut) , Price: 9

Best Price for the rod of length 4: 10

Approach:

Naive Approach: Recursion

• There can be n-1 cuts can be made in the rod of length n, so there are 2^n-1 ways to cut the rod.
• So for every length, we have 2 options either we cut it or not. we will consider both options and choose the optimal out of it.

Time Complexity: O(2^n-1)
But this time complexity is very high since we are solving many subproblems repeatedly.

Run This Code

Code:

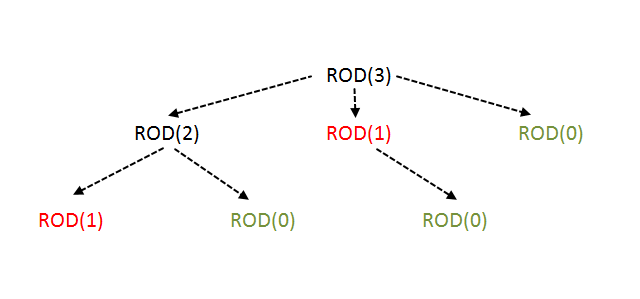
Dynamic Programming: Bottom-Up

Instead of solving the sub-problems repeatedly we can store the results of it in an array and use it further rather than solving them again.

See the Code for a better explanation:

Run This Code

Code:

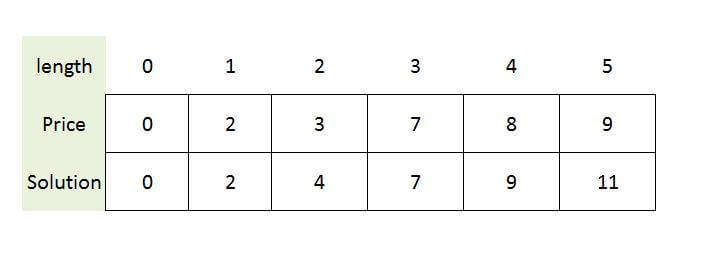
Result: Max profit for length is 5:11

Reference: Link