|
Be the first user to complete this post
|
Add to List |
201. Dynamic Programming - Split the String into Minimum number of Palindromes.
Objective:
You are given a large string. You need to cut the string into chunks such that each substring that you get is a palindrome. Remember that each 1 length string is always a palindrome. You need to find the minimum number of cuts that you need to make such that each substring is a palindrome.
Example:
String x = "xabaay" 5 cuts makes all the substrings palindrome : x, a, b, a, a, y 4 cuts makes all the substrings palindrome : x, a, b, aa, y 3 cuts makes all the substrings palindrome : x, aba, a, y Output: 3 cuts
Approach:
Using Recursion:
We need to try all the cuts which make all the substrings palindrome and then we will choose the minimum number of cuts required.
- Check if the entire string is a palindrome, if yes then return 0 ( no cuts required).
- If step 1 fails means it's not a palindrome then split the string into two parts in every possible way (ex: String is "xaab" then all possible splits are "x, aab", "xa, ab", "xaa, b") and solve these two parts recursively till substring not found to be a palindrome. Each time you make a split, add 1 to the number of cuts.
- Choose the minimum cuts in step 2.
- See the diagram for more understanding.
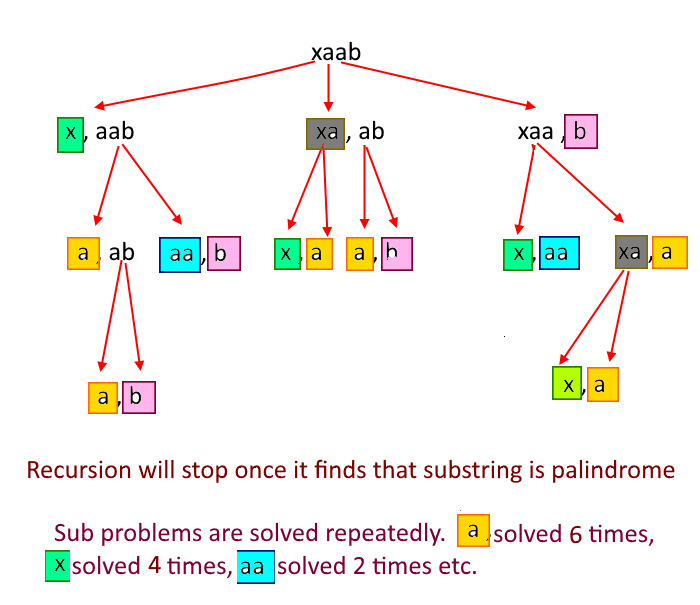
Time Complexity: If there are n characters in the string then n-1 cuts can be made and for every cut we have two options, whether cut or not. so time complexity will be 2(n-1).
Recursion Code:
Output:
Recursion- Cuts Required: 3 Recursion- Time Taken(ms): 345
Using Dynamic Programming:
As we have seen in the diagram above many problems are solved repeatedly. So we can apply the Top-down approach.
We will use Hash Map and store the solution of subproblems. So every time we make a cut, we check whether we have already solved the subproblem by checking its entry in Hash Map, if yes then use it and if not then solve it and store it in HashMap for future use.
Now, this way every problem will be solved only once. Time Complexity will be a number of subproblems so it will O(N2).
NOTE: We have compared the running time of recursion and dynamic programming in the output.
Output:
Dynamic Programming- Cuts Required: 3 Dynamic Programming- Time Taken(ms): 2
NOTE: As you can see Dynamic Programming is way faster than Recursion.

