|
This post is completed by 1 user
|
Add to List |
104. Print the Bottom View of a Binary Tree
What is Bottom View: The bottom view of a binary tree represents the nodes visible when viewing the tree from the bottom-up perspective. In other words, it displays the nodes that are at the bottommost position at each horizontal distance from the root. This view provides valuable insights into the structure of the tree, revealing the nodes that are most significant in terms of their vertical position. See the example below.
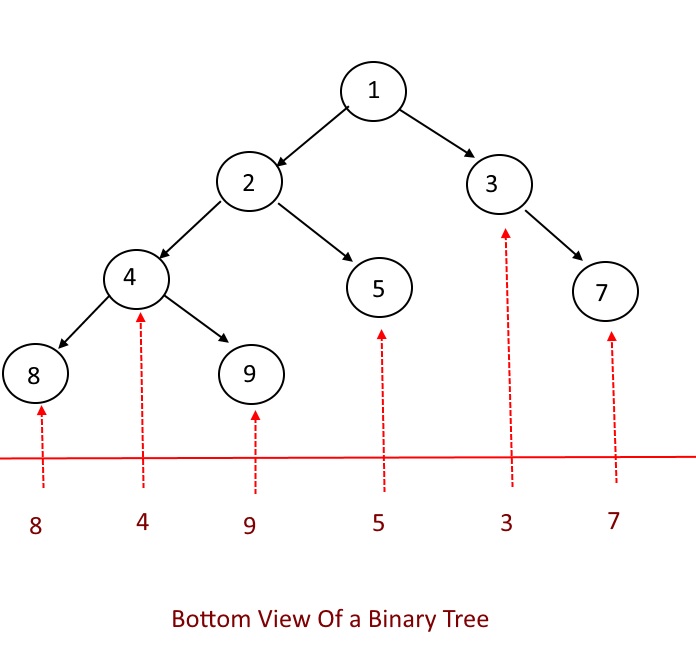
as you can see in the example above,8, 4, 9, 5, 3, 7 is the bottom view of the given binary tree.
Approach:
This approach is quite similar to the - Print the Binary Tree in Vertical Order Path.
and Print The Top View of a Binary Tree.
To categorize the tree elements vertically, use a variable named level. Increment level whenever you move left and decrement it whenever you move right.
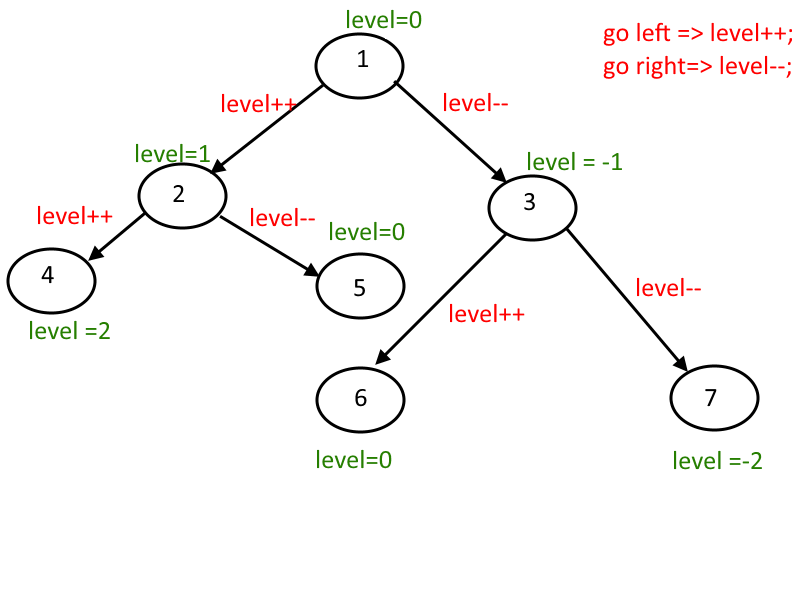
Following the steps above, the levels are now separated vertically. Next, you need to store the elements of each level. To do this, create a map or dictionary where the key-value pair represents the level and the element at that level, respectively.
Now, perform a level-order traversal and store only the most recently visited node at each level. This ensures that only the last element at each level is stored.
For the level-order traversal or Breadth-First Search (BFS), utilize a simple queue technique. Create a class called QueuePack to store objects containing the node and its level.
Finally, traverse through the map and print all the values stored in it. This output will represent the bottom view of the tree.
Note: Use TreeMap in case you want to print the bottom view in order.
Output:
5 9 3 4 7 8

