|
This post is completed by 1 user
|
Add to List |
161. The Word Break Problem
Objective: Given a string and a dictionary of words, find out if the input string can be broken into a space-separated sequence of one or more dictionary words.
Example:
dictionary = [I , have, tutorial, horizon, am, this, dog] String = Iamtutorialhorizon Output: I am Sumit String =thisisadog Output : String can't be broken
Approach: Backtracking- Naive Approach
- Navigate the given input string.
- Take a blank string and keep adding one character at a time to it.
- Keep checking if the word exists in the dictionary.
- If a word exists in the dictionary then add that word to the answer string and make a recursive call to the rest of the string.
- If any of the recursive calls return false then backtrack and remove the word from the answer string and again keep adding the characters to the string.
- If all the recursive calls return true that means the string has been broken successfully.
- See the code for a better explanation.
If we notice here we are solving many sub-problems repeatedly.
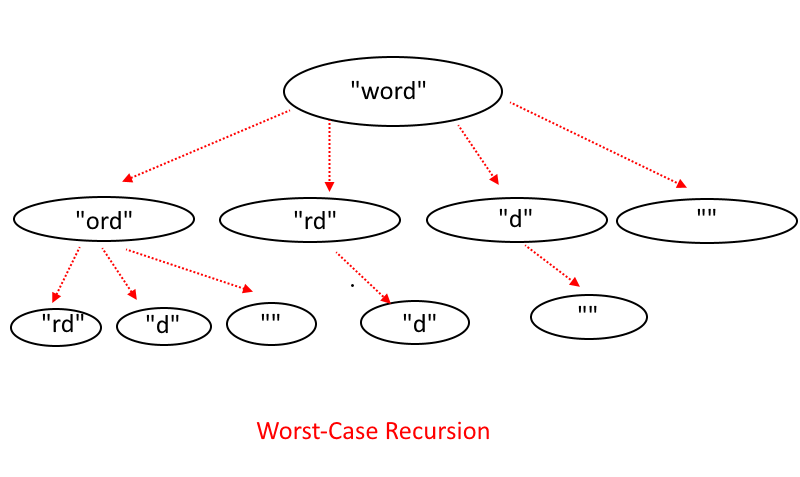
Dynamic Programming to Rescue:
- We will use top-down approach.
- Before we solve it for any string check if we have already solve it.
- We can use another HashMap to store the result of already solved strings.
- Whenever any recursive call returns false, store that string in HashMap.
- See the code for a better explanation
Output:
Output: this is sumit jain

