|
Be the first user to complete this post
|
Add to List |
444. Articulation Points OR Cut Vertices in a Graph
Objective: Given a graph, write an algorithm to find all the articulation points or cut vertices.
Articulation Points: In a graph, a vertex is called an articulation point if removal of that vertex (along with all the edges associated with that vertex) increases the number of connected components or in other words, removal of that vertex makes the graph disconnected. It is also called a cut vertex. See the example below
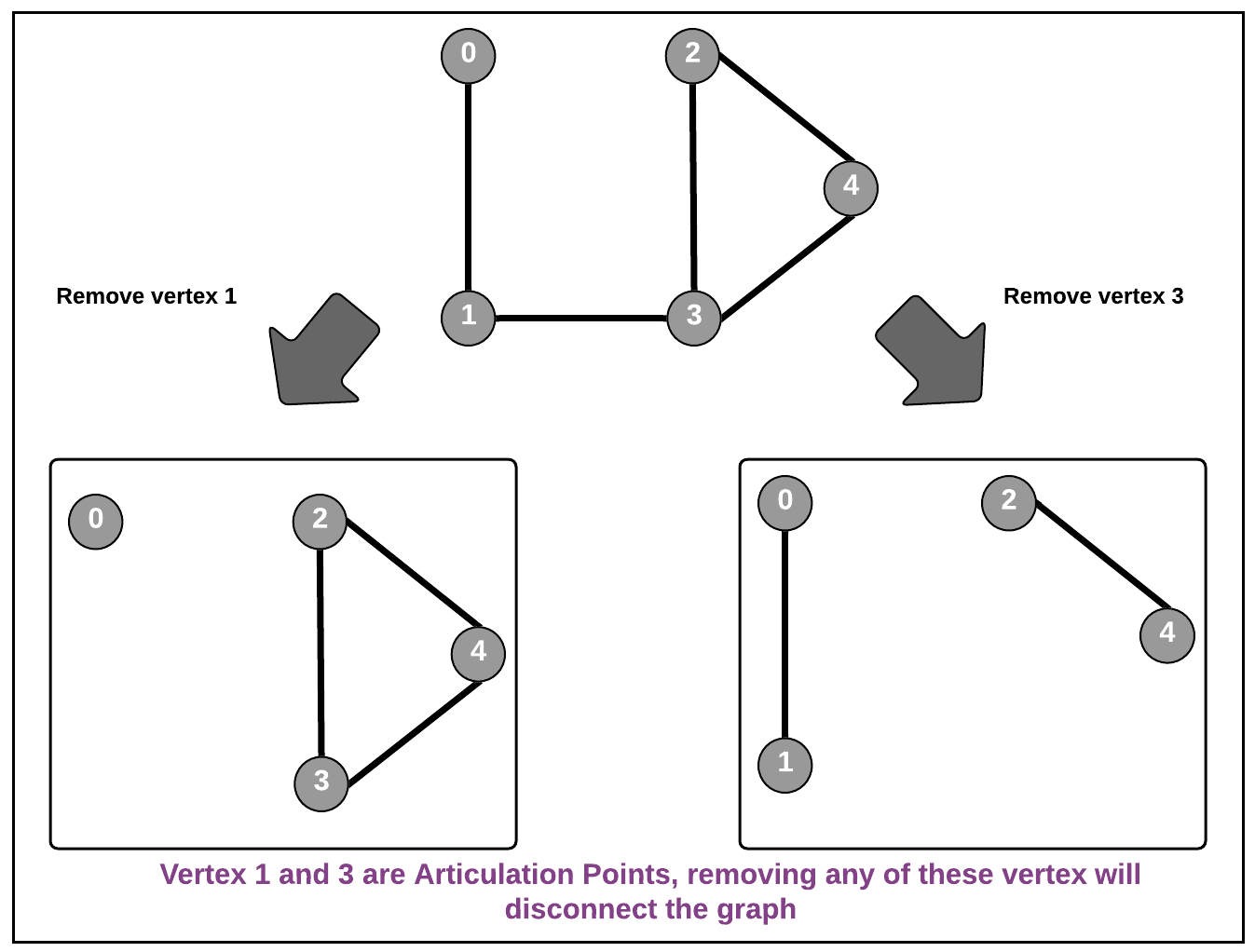
In the example above, either vertex 1 or vertex 3 is removed (along with the edges associated with the vertex) the graph will split into multiple connected graphs.
Why do we care:
Articulation points or cut vertices represent vulnerabilities in the network. Basically, it tells about failures in the network and if that happens, your network will be split and disconnected.
Approach:
Brute Force:
- Iterate through all the vertices.
- Remove the current vertex
- Check if the graph is disconnected (read - check disconnectivity in the graph).
- If yes then the current vertex is an articulation point, print it.
- Add the removed vertex back to the graph.
- Once the iteration is completed, all the articulation points are found.
Time Complexity: O(V) for iterating through all the vertices and O(V+E) for each DFS. so overall time complexity will be O(Vx(V+E))
Better Solution: Single DFS using Back Edge
The problem can be solved in single DFS (Depth-First Search) using the back edge. Let's first understand what is the back edge.
Back Edge: An edge that connects a vertex to the vertex which gets traversed before its parent vertex.
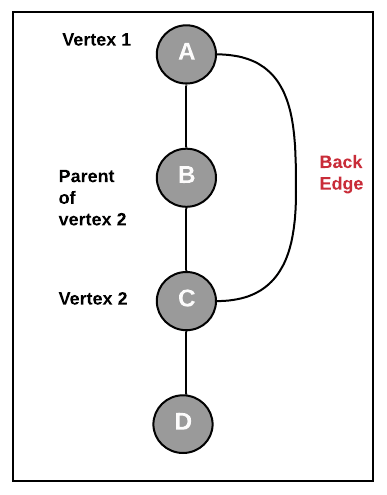
See the example above where vertex C has a parent as vertex B but there is an edge from A to C so If we are traversing from vertex A, vertex C can be traversed before vertex B. So edge connecting A and C is back edge.
Why back edge matters: Back edge matters since it makes sure that the graph will stay connected even if parent vertex is removed from the graph. As in the picture above if we do not have the back edge (edge A-C) then removal of vertex B will disconnect the graph and in the presence of edge A-C, even after removal of vertex B, the graph will be connected. See another example below, where edge B-D is the back edge. If this edge is not present then removal of vertex B will disconnect the graph (edge B-C can be considered as a back edge).
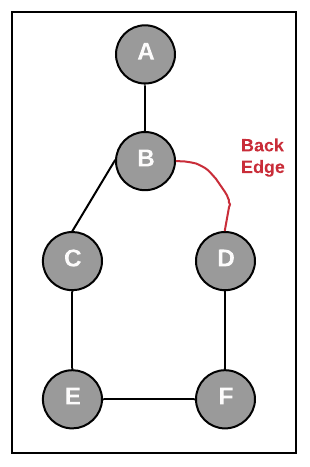
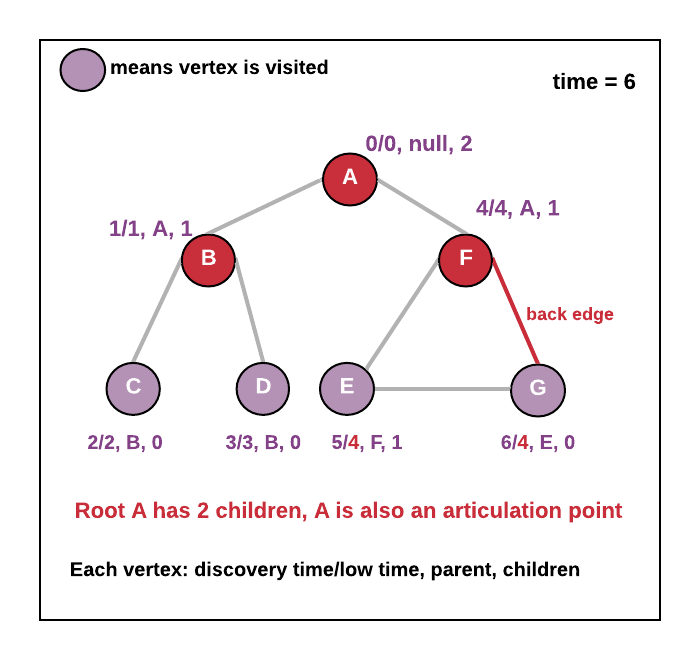
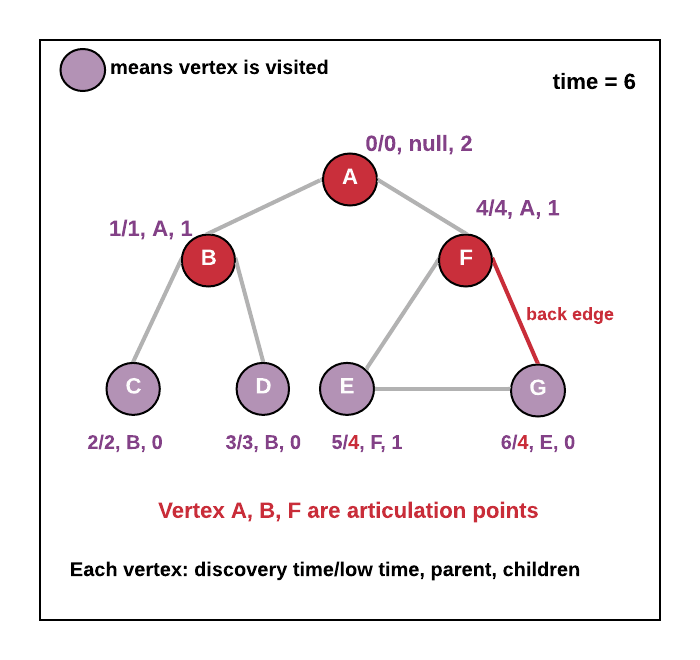
But what about root vertex: Root vertex will not have parent vertex so there cannot be any back edge, so checking if root vertex is articulation point just check if root has more than one child then the root is an articulation point (since removing root will disconnect all the subtrees of the root).
Note: Let's say if root u and two children v1 and v2 and any vertex is subtree v1 has an edge to some vertex in subtree v2 then removing root u will not disconnect the v1 and v2 but in this case v1 and v2 will not be considered as two children, it will be considered as only one child which has a back edge to root. See the examples below
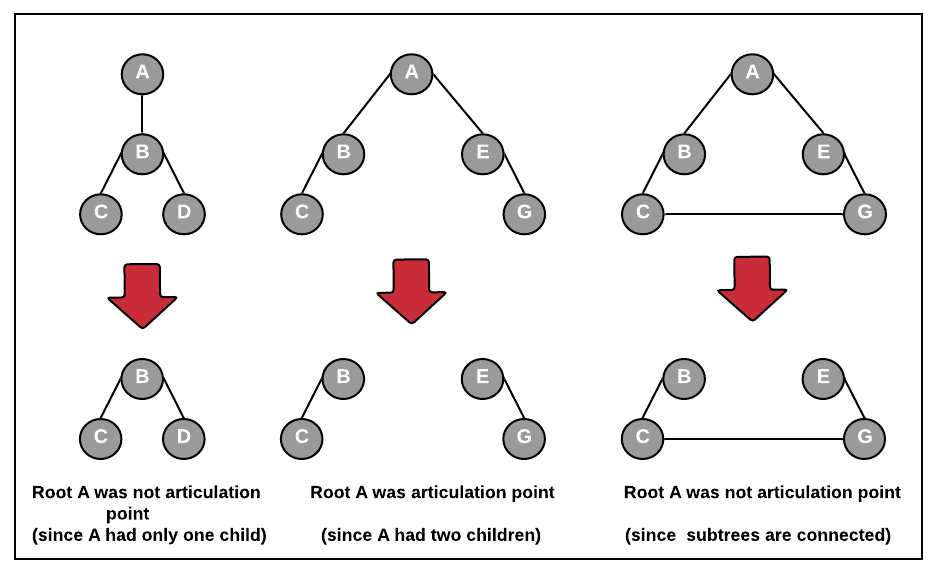
Summarized Algorithm:
Do the Depth-First Search starting from root vertex. During DFS, if for any vertex, any of the below conditions is true then that vertex is articulation point or cut vertex.
- Vertex v is the root and has two children.
- If Vertex v is not the root and there is no back edge from any vertex from subtree rooted as v to either one of the ancestors of vertex v or to the vertex v itself..
Steps to implement the algorithm
- We will maintain the information below for each vertex v
- time - the first time a vertex was visited. Initialize time = 0.
- discoveryTime - First time during DFS, a vertex is reached. (for root vertex it will be 0).
- lowTime - The visit time of the earliest visited vertex to which there is a back edge from any vertex in the subtree rooted at vertex v.
- parent - stores the parent of the current vertex.
- child - no of children for vertex (will be useful only for root).
- visited[]- boolean array keeps tracks whether the vertex is visited or not.
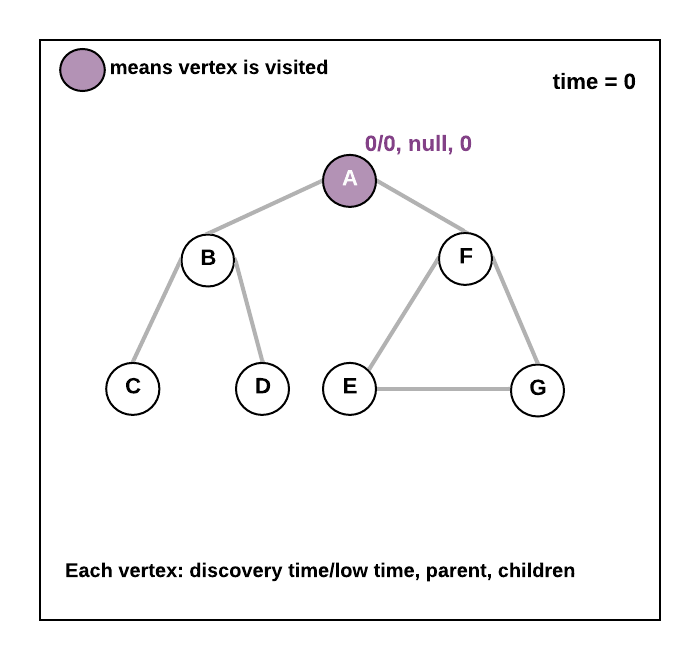
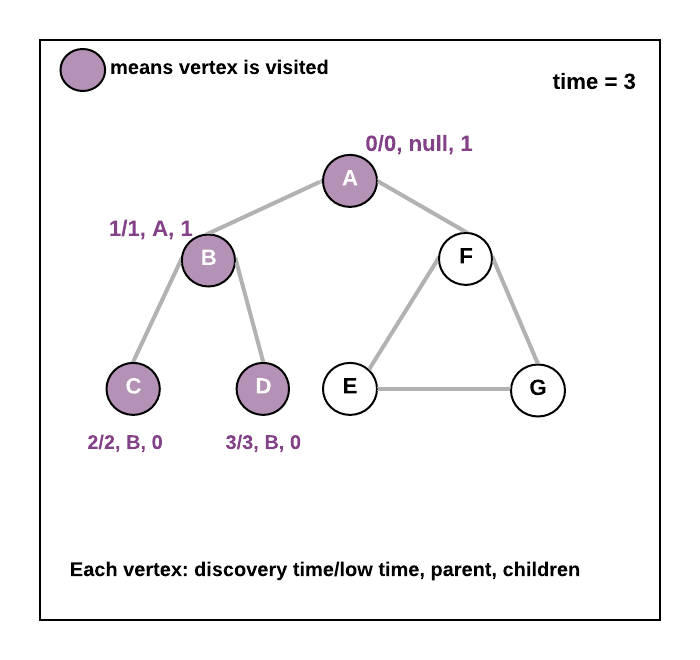
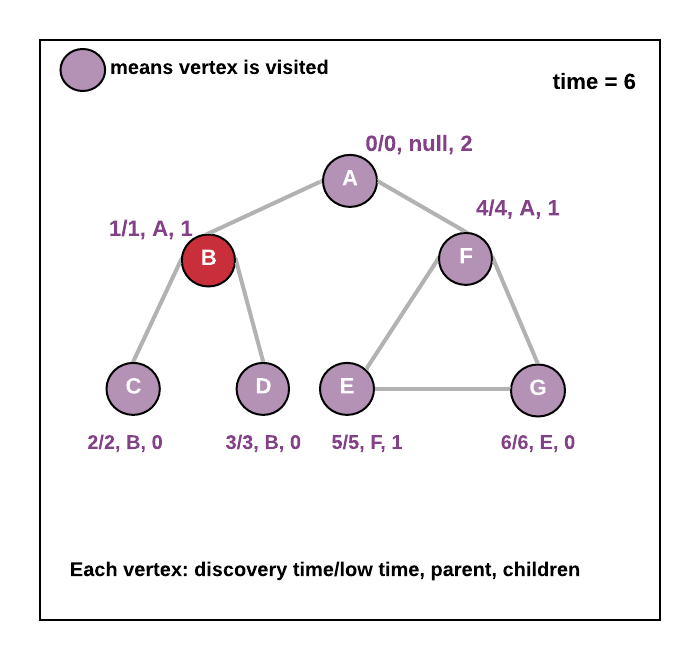
- Do the Depth-First Search starting from root vertex. (choose any vertex as root). So for root vertex, lowTime=0, discoveryTime=0, time=0, mark root vertex in visited[] array and parent as null. Now traverse all the adjacent vertices of root
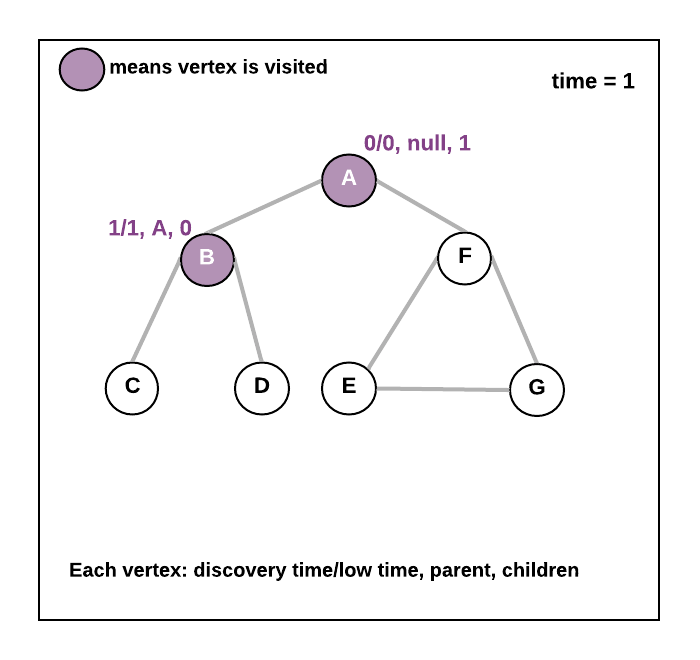
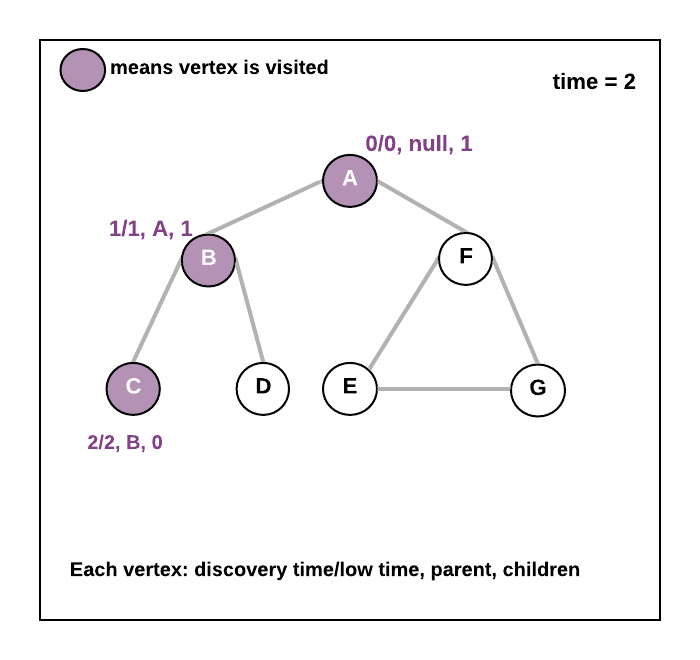
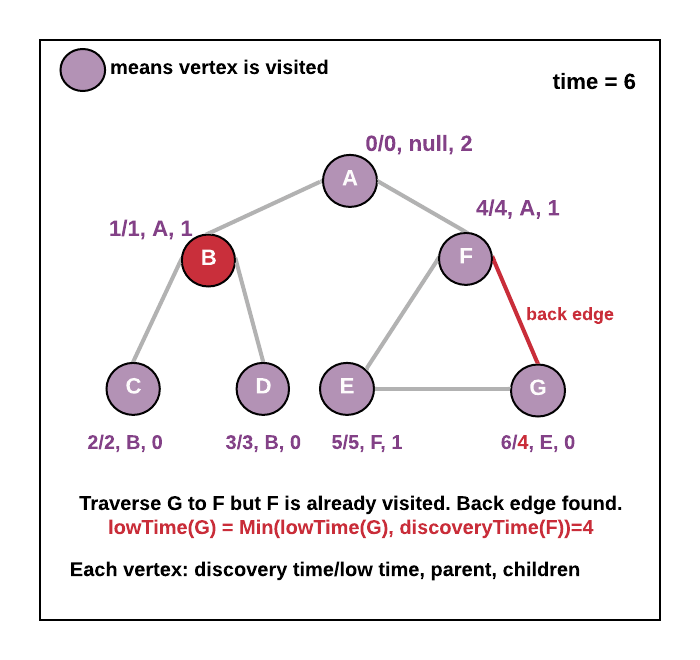
- As you move to an adjacent vertex v1, do time++ and now put lowTime=discoveryTime=time=1, parent = root vertex, visited[v1]=true. Now make a recursive call from vertex v1. Now traverse all the adjacent vertices of , as you move to the next adjacent vertex v2, again do time++ and put lowTime=discoveryTime=time=2, parent = v1, visited[v2]=true. Repeat the same process until all the vertices are marked in the visited array. During this DFS traversal for any vertex x if you find an adjacent vertex y which is already visited ( visited[y]=true and parent[y]!=x ) earlier that means we have found the back edge in that case update lowtime of the current vertex = minimum(lowtime of the current vertex, discoveryTime of adjacent vertex) . Also, keep track of no of children for each vertex.
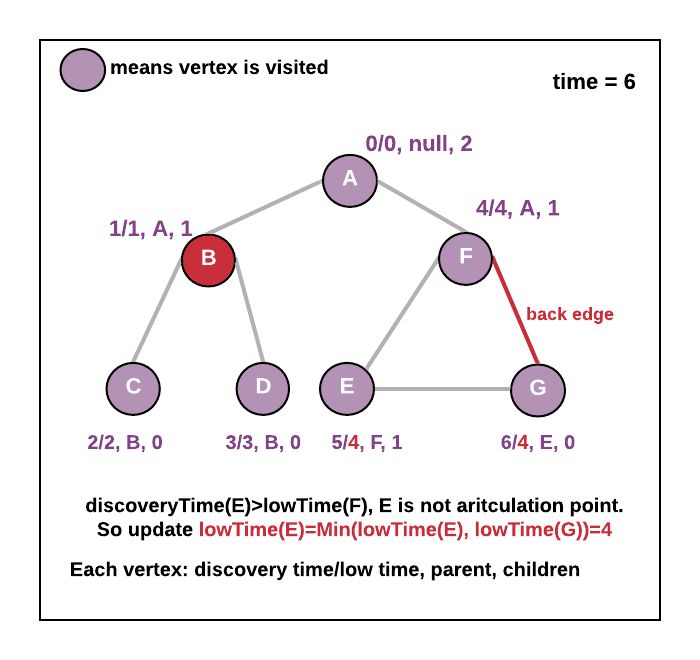
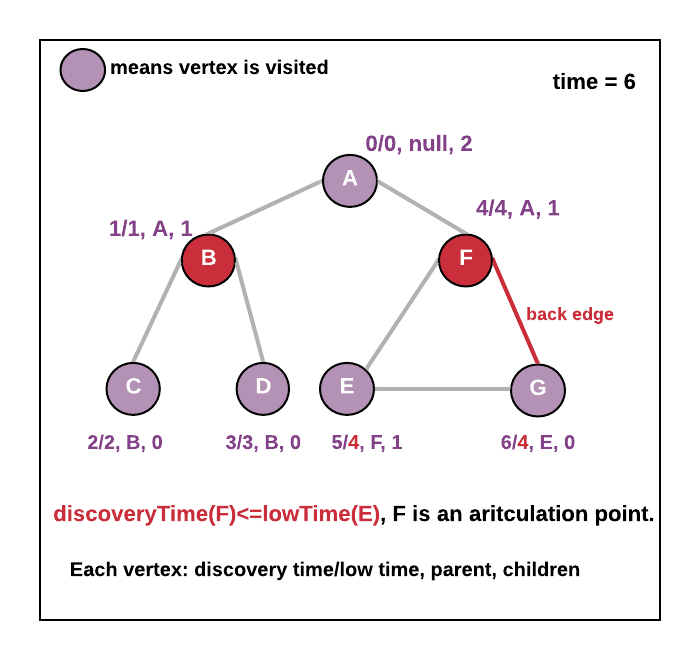
- During tail recursion - while coming back from recursion-
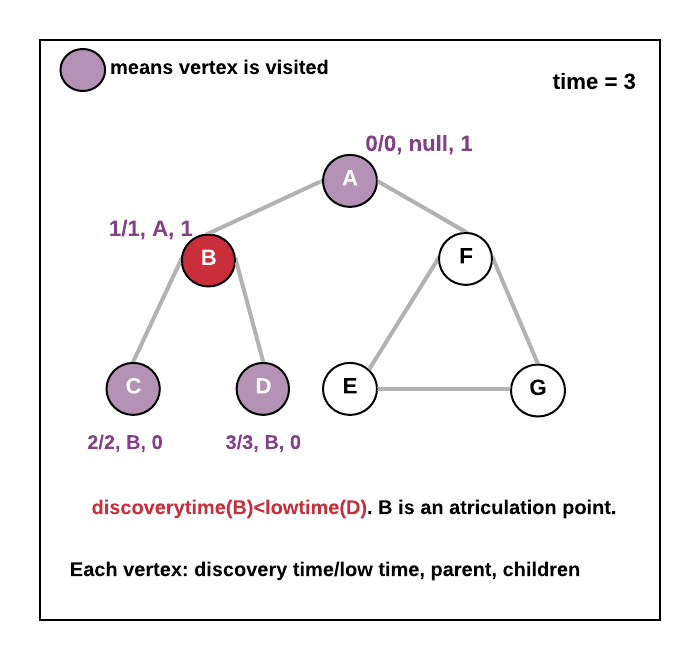
- If you find vertex v where discoveryTime(v) <= lowTime(adjacent vertex of v) then v is an articulation point if v is not a root.
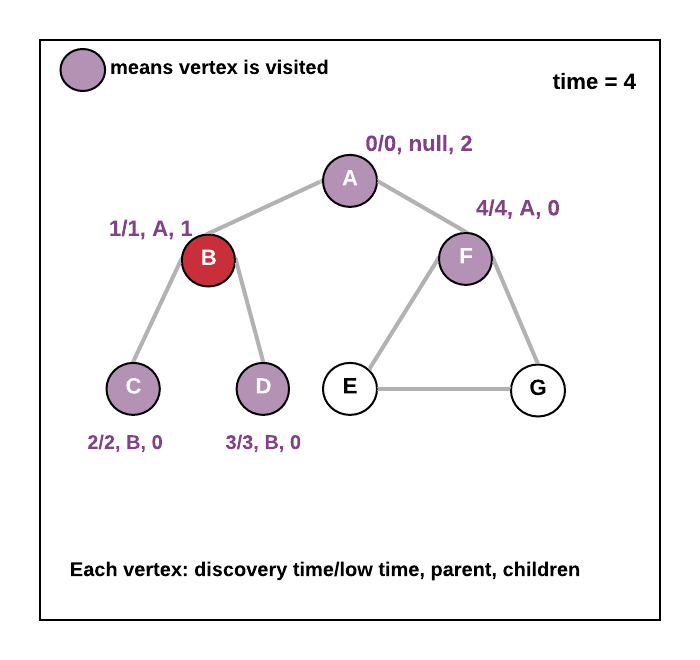
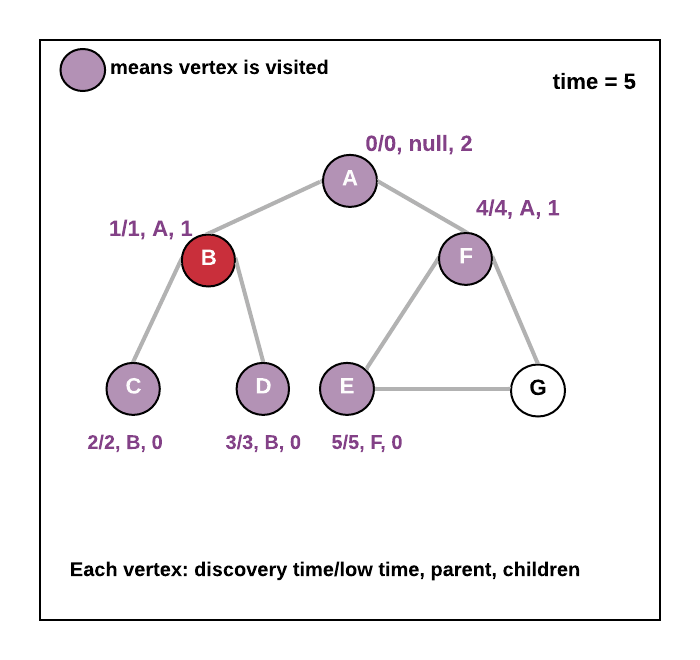
- Else - means discoveryTime(v) > lowTime(adjacent vertex of v) in that case update the lowTime of v. lowtime(v)= minimum(lowTime(v), lowtime(adjacent vertex of v).
- if vertex is root vertex and had two children then it is an articulation point.
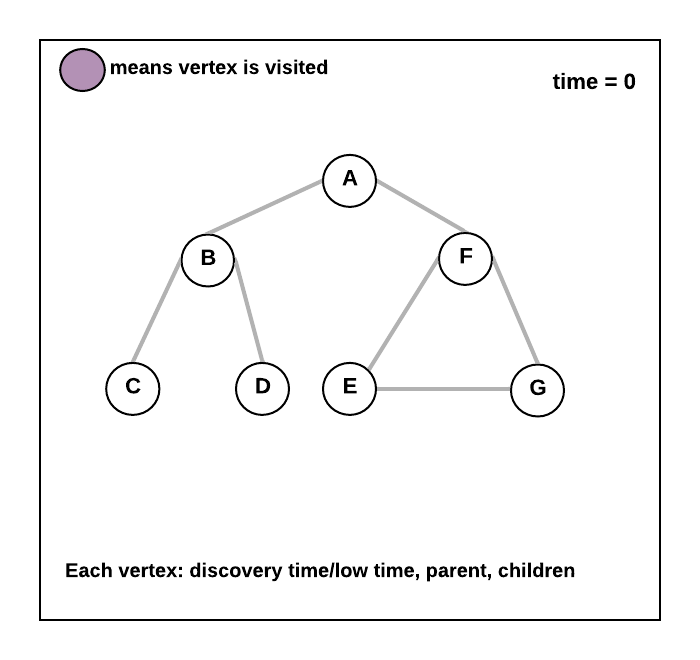
- See the animation below.
Output:
Articulation Points are: [2, 1, 0]
Reference:
- https://www.hackerearth.com/practice/algorithms/graphs/articulation-points-and-bridges/tutorial/
- https://www.youtube.com/watch?v=2kREIkF9UAs