|
Be the first user to complete this post
|
Add to List |
100. AVL Tree - Insertion
What is AVL Tree :
AVL tree is widely known as a self-balancing binary search tree. It is named after its creator (Georgy Adelson-Velsky and Landis' tree). In AVL Tree, the heights of child subtrees at any node differ by at most 1. At any time if height difference becomes greater than 1 then tree balancing is done to restore its property.
Search, Insertion, and deletion, all operations take O(logn) time since the tree is balanced.
Why AVL Tree is better than normal Binary Search Tree:
Average time complexity in binary search tree for any operation takes O(logn) time but there are times when your tree is skewed. In those cases, the operations on them take O(n) time but in AVL Tree, since it is always balanced, it always takes O(logn) time.
How Tree balanced itself:
There are two basic operations, using which tree balanced itself.
- Left Rotation
- Right Rotation.
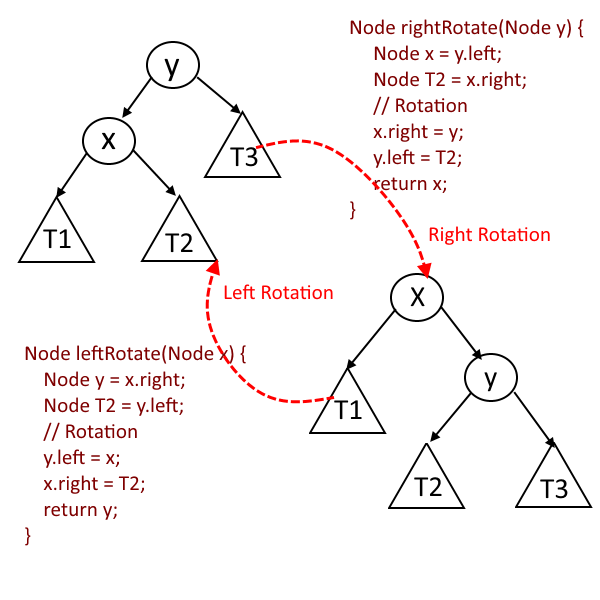
How These Rotation works to balance the tree:
- Let 'A' be the new node added to the tree.
- Once 'A' is added, start traveling up from 'A' to root and find the unbalanced node, balance it and again keep traveling up.
- Say you have found the node z which is unbalanced.
- Node y is the child of z and x be the grandchild of z.
Then there will be four possibilities
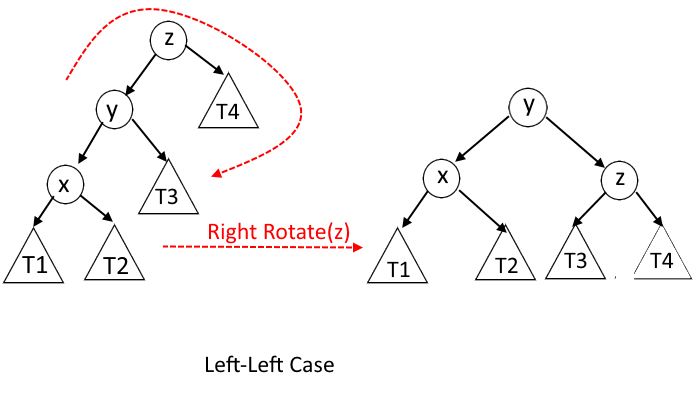
- Left-Left Case: - x is the left child of y and y is the left child of z.
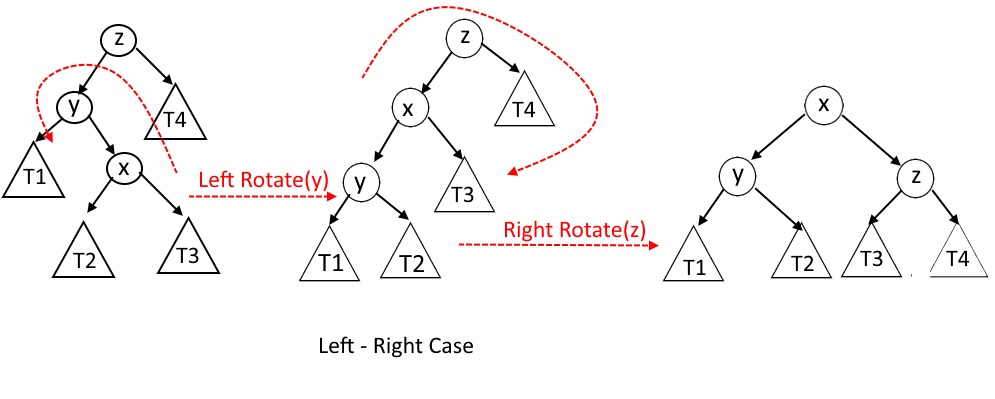
- Left-Right Case: - x is the right child of y and y is the left child of z.
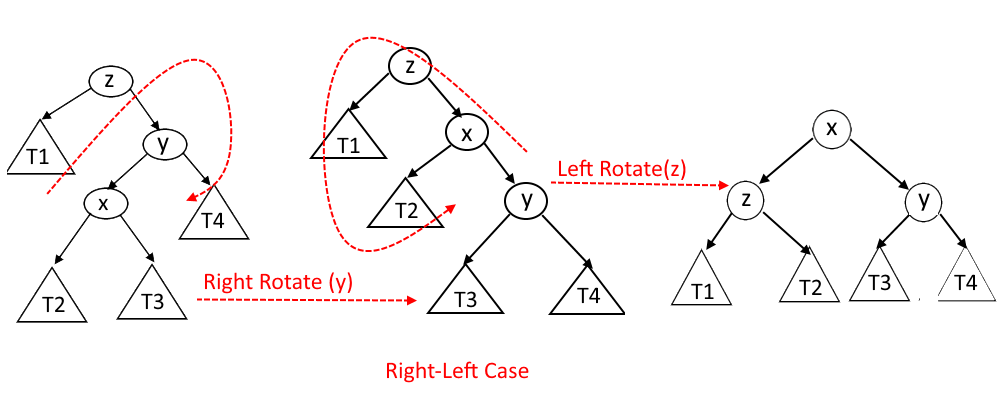
- Right-Left Case: - x is the left child of y and y is the right child of z.
- Right-Right Case: - x is the right child of y and y is the right child of z.
Left-Left Case : - x is the left child of y and y is the left child of z.
Left-Right Case : - x is the right child of y and y is the left child of z.
Right-Left Case: - x is the left child of y and y is the right child of z.
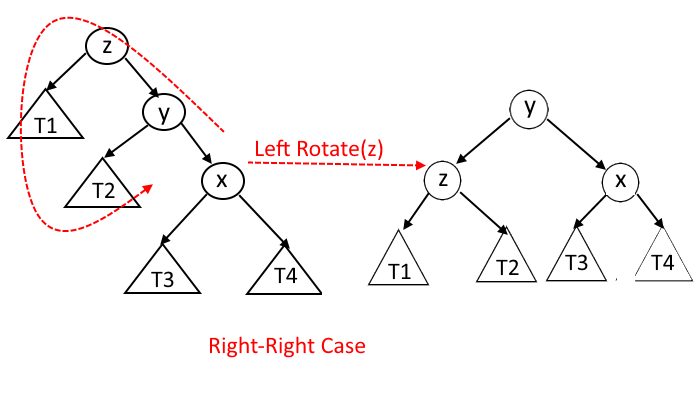
Right-Right Case: - x is the right child of y and y is the right child of z.
Insertion Operation:
- Insert the new Node using recursion so that while backtracking you will all the parent's nodes to check whether they are still balanced or not.
- Every node has a field called height with a default value of 1.
- When a new node is added, its parent's node height gets increased by 1.
- So as mentioned in step 1, every ancestor's height will get updated while backtracking to the root.
- At every node, the balance factor will also be checked. balance factor = (height of left Subtree - the height of right Subtree).
- If the balance factor =1 means the tree is balanced at that node.
- If the balance factor >1 means the tree is not balanced at that node, the left height is more than the right height so that means we need rotation. (Either Left-Left Case or Left-Right Case).
- Say the current node which we are checking is X and If the new node is less than the X.left then it will be the Left-Left case, and if the new node is greater than the X.left then it will be the Left-Right case. See the pictures above.
- If the balance factor <-1 means the tree is not balanced at that node, the right height is more than the left height so that means we need rotation. (Either Right-Right Case or Right-Left Case)
- Say the current node that we are checking is X and If the new node is less than the X.right then it will be Right-Right case, and if the new node is greater than the X.right then it will be the Right-Left case. See the pictures above.
Output:
Inorder Traversal of Constructed AVL Tree : 1 2 4 5 6 9 10 11 14 20 New Root of AVL Tree is : 5

