|
This post is completed by 2 users
|
Add to List |
149. Backtracking - Rat In A Maze Puzzle
Given a maze, NxN matrix. A rat has to find a path from source to destination. maze[0][0] (left top corner)is the source and maze[N-1][N-1](right bottom corner) is destination. There are a few cells that are blocked, which means the rat cannot enter those cells. The rat can move in any direction ( left, right, up, and down).
Input: A 2D matrix with 0's and 1's filled in it. 0 means that the cell is blocked and 1 means the rat can move to that cell.
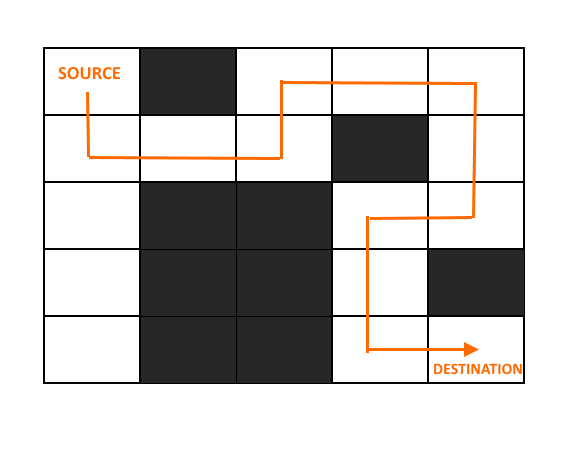
Approach:
- Create a solution matrix of the same structure as the maze.
- Whenever the rat moves to a cell in a maze, mark that particular cell in the solution matrix.
- At the end print the solution matrix, and follow the 1's from the top left corner, it will be that path for the rat.
Algorithm:
- If the rat reaches the destination
- Print the solution matrix.
- Else:
- Mark the current cell in the solution matrix as 1.
- Move downwards and recursively check if this movement leads to the solution.
- If movement in the above step doesn't lead to the solution then go towards the right and recursively check if this movement leads to the solution.
- If movement in the above step doesn't lead to the solution then move upwards and recursively check if this movement leads to the solution.
- If movement in the above step doesn't lead to the solution then move in the left direction and recursively check if this movement leads to the solution.
- If none of the above solutions works then BACKTRACK and mark the current cell as 0.
- In each recursive call, check the conditions like the rat is not crossing the matrix boundaries and not visiting the already visited cell.
If the rat runs out of options, return false because it's not possible to reach to the destination
Output:
1 0 1 1 1 1 1 1 0 1 0 0 0 1 1 0 0 0 1 0 0 0 0 1 1
Reference: http://www.geeksforgeeks.org/backttracking-set-2-rat-in-a-maze/

