|
This post is completed by 1 user
|
Add to List |
158. Backtracking - Search a Word In a Matrix
Objective: Given a 2D matrix of characters. Check whether the word exists in the matrix or not. If it exists then print its path. All movements are allowed (right, left, up, down, and diagonally).
Example:

Approach:
We will show the path as an increment counter
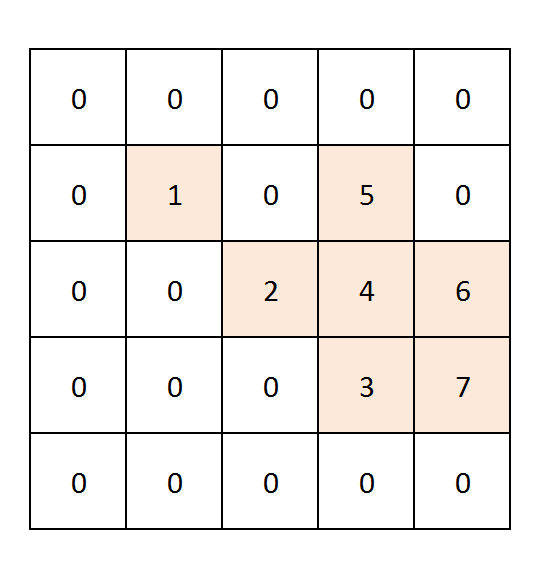
- Create a solution matrix of the same structure as the Matrix.
- Try each cell as a starting point.
- Check current cell is not already used and the character in it matches with the character in the word at index (starts will 0).
- Check if index = length of the word, means we have found the word. return true and print the solution matrix.
- If the above criteria match, mark that cell with a number Whenever any cell matches the criteria, put a number corresponding to it in the solution matrix. (start with 0 and keep incrementing it, it will show us the path for the word).
- Now try to solve the rest of the problem recursively by making index +1. Check all 8 directions ( up, down, left, right, diagonally up-left, diagonally up-right, diagonally down-left, diagonally down-right). Check the boundary conditions as well
- If none of the 8 recursive calls return true, BACKTRACK and undo the changes ( put 0 to the corresponding cell in solution matrix) and return false.
- Choose a different starting point.
- If all the starting points tried and solution not found, return false
- See the code for a better understanding.
Output:
0 0 0 0 0 0 1 0 5 0 0 0 2 4 6 0 0 0 3 7 0 0 0 0 0

