|
This post is completed by 1 user
|
Add to List |
77. Construct a binary tree from given Inorder and Postorder Traversal
Objective: - Given a inorder and postorder traversal, write an algorithm to construct a binary tree from that. This problem was asked in the Microsoft coding competition.
Input: Inorder and postorder traversals
Similar Problems: Make a Binary Tree from Given Inorder and Preorder Traveral.
Appraoch:
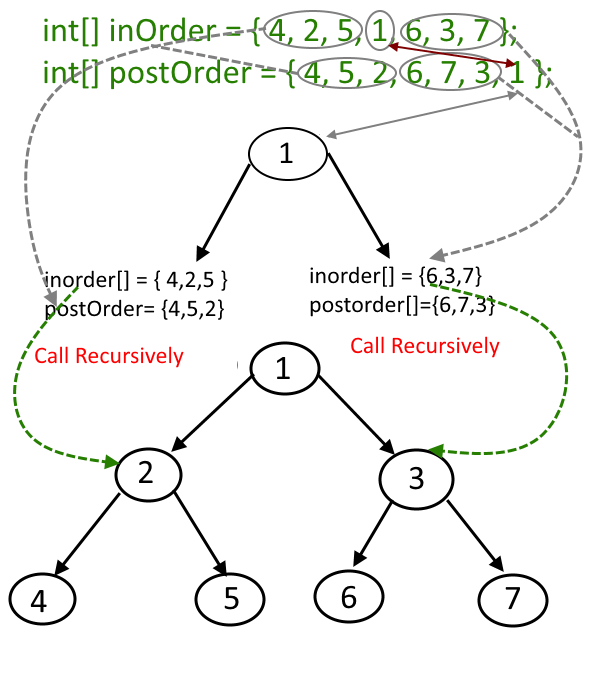
int[] inOrder = { 4, 2, 5, 1, 6, 3, 7 };
int[] postOrder = { 4, 5, 2, 6, 7, 3, 1 };.
- Last element in the postorder [] will be the root of the tree, here it is 1.
- Now the search element 1 in inorder[], say you find it at position i, once you find it, make note of elements which are left to i (this will construct the leftsubtree) and elements which are right to i ( this will construct the rightSubtree).
- Suppose in previous step, there are X number of elements which are left of 'i' (which will construct the leftsubtree), take first X elements from the postorder[] traversal, this will be the post order traversal for elements which are left to i. similarly if there are Y number of elements which are right of 'i' (which will construct the rightsubtree), take next Y elements, after X elements from the postorder[] traversal, this will be the post order traversal for elements which are right to i
- From previous two steps construct the left and right subtree and link it to root.left and root.right respectively.
- See the picture for better explanation.
Output:
inorder traversal of constructed tree : 4 2 5 1 6 3 7

