|
Be the first user to complete this post
|
Add to List |
197. Convert Binary Tree into Threaded Binary Tree
Objective: Given a binary tree write an algorithm to convert it into a threaded binary tree.
Note: The tree node has an extra Boolean field to be used.
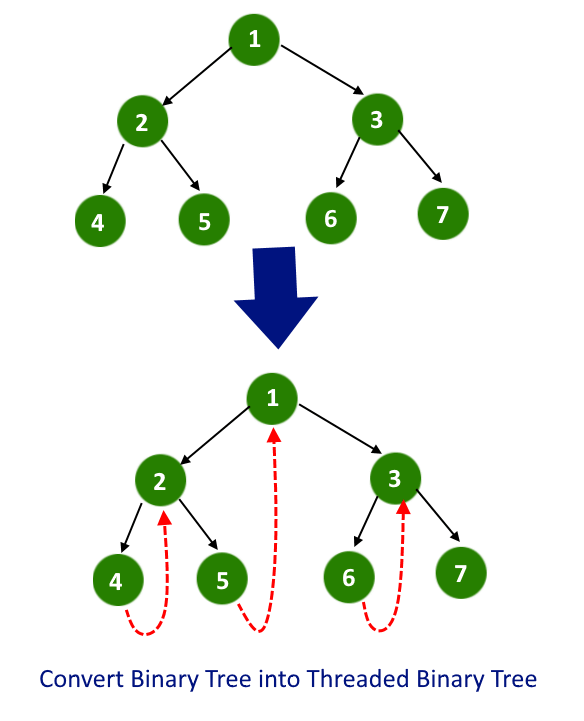
In an earlier article "Introduction to Threaded Binary Tree" we have seen what is a threaded binary tree, its types of it and what advantages it has over normal binary trees. In this article, we will see how to convert existing binary trees to threaded binary trees. we will convert it to a single-threaded binary tree.
- Binary trees have a lot of wasted space: the leaf nodes each have 2 null pointers. We can use these pointers to help us in inorder traversals.
- A threaded binary tree makes the tree traversal faster since we do not need stack or recursion for traversal
Single Threaded: each node is threaded towards either the in-order predecessor or successor (left or right) means all right null pointers will point to inorder successor OR all left null pointers will point to inorder predecessor.
So in this article, we will put all right null pointers to its inorder successor.
Approach:
Solution 1: we can do the inorder traversal and store it in some queue. Do another inorder traversal and where ever you find a node whose right reference is NULL, take the front element from the queue and make it the right of the current node. (Reference: http://www.geeksforgeeks.org/convert-binary-tree-threaded-binary-tree/)
Better Solution:
The problem with the earlier solution is it's using the extra space for storing the inorder traversal and using two traversals.
Now we will see the solution which will convert the binary trees into a threaded binary tree in one single traversal with no extra space required.
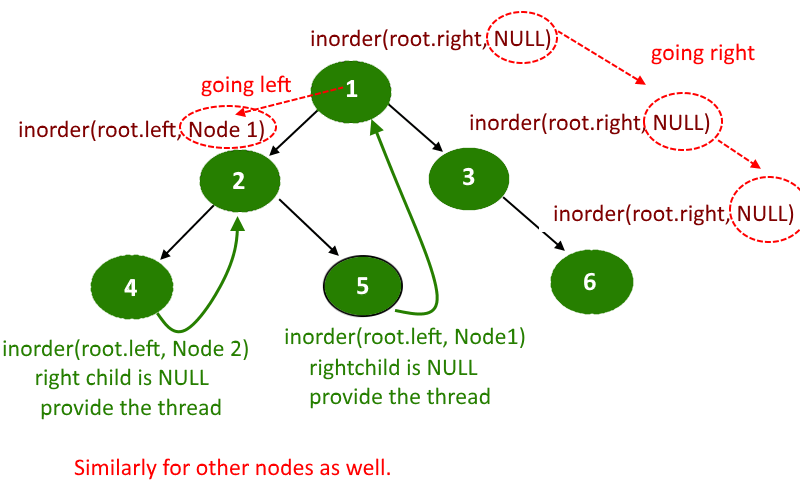
- Do the reverse inorder traversal, which means visiting the right child first.
- In the recursive call, pass an additional parameter, the node visited previously.
- whenever you will find a node whose right pointer is NULL and the previously visited node is not NULL then make the right of node points to the previously visited node and mark the boolean rightThreaded as true.
- The important point is whenever making a recursive call to the right subtree, do not change the previous visited not, and when making a recursive call to the left subtree then pass the actual previous visited node. see the image below
Read the complete code and try it in our IDE for a better understanding.
Output:
Inorder Traversal: 1 5 7 10 12 15 20

