|
This post is completed by 1 user
|
Add to List |
365. Convert Infix to Postfix Expression
Objective: Given an Infix expression, write an algorithm to convert it into Postfix expression.
Example:
Input: Infix expression - A + B Output: Postfix expression- AB+ Input: Infix expression - A+B*(C^D-E) Output: Postfix expression- ABCD^E-*+
Approach: Use Stacks
- Operator stack: This stack will be used to keep operations (+, -, *, /, ^)
Order of precedence of operations-
- ^ (Exponential)
- / *
- + -
Note: brackets ( ) are used to override these rules.
Algorithm:
Initialize result as a blank string, Iterate through given expression, one character at a time
- If the character is an operand, add it to the result.
- If the character is an operator.
- If the operator stack is empty then push it to the operator stack.
- Else If the operator stack is not empty,
- If the operator's precedence is greater than or equal to the precedence of the stack top of the operator stack, then push the character to the operator stack.
- If the operator's precedence is less than the precedence of the stack top of operator stack then "pop out an operator from the stack and add it to the result until the stack is empty or operator's precedence is greater than or equal to the precedence of the stack top of operator stack". then push the operator to stack.
- If the character is "(", then push it onto the operator stack.
- If the character is ")", then "pop out an operator from the stack and add it to the result until the corresponding "(" is encountered in operator stack. Now just pop out the "(".
Once the expression iteration is completed and the operator stack is not empty, "pop out an operator from the stack and add it to the result" until the operator stack is empty. The result will be our answer, postfix expression.
Please see the walkthrough of an example below for more understanding.
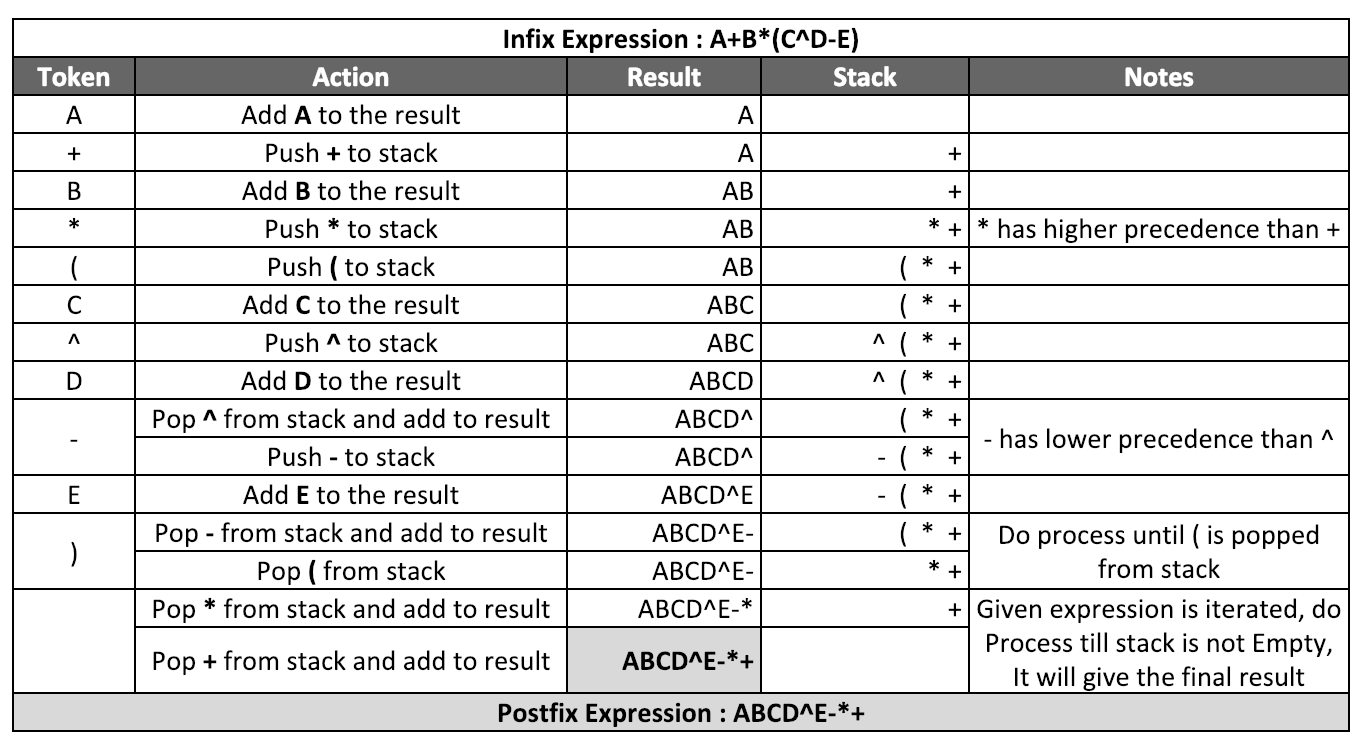
We recommend to read about infix and postfix expressions if these terms are new to you.
Output:
Infix Expression: A+B*(C^D-E) Postfix Expression: ABCD^E-*+

