|
Be the first user to complete this post
|
Add to List |
196. Double Threaded Binary Tree Complete Implementation
In an earlier article "Introduction to Threaded Binary Tree" we have seen what is a threaded binary tree, its types and what advantages it has over normal binary trees.
In this article, we will see the complete implementation of a double-threaded binary tree. ( Click here to read about "single threaded binary tree")
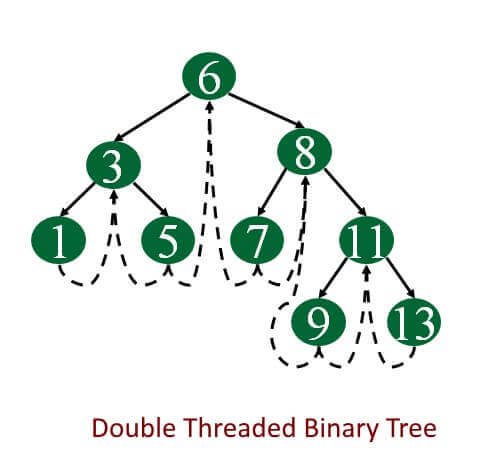
Image Source: http://web.eecs.umich.edu/~akamil/teaching/su02/080802.ppt
Double threaded: each node is threaded towards both the in-order predecessor and successor (left and right) means all right null pointers will point to the in-order successor AND all left null pointers will point to the in-order predecessor.
Implementation:
Let's see how the Node structure will look like
class Node {
int data;
int leftBit;
int rightBit;
Node left;
Node right;
public Node(int data) {
this.data = data;
}
}
If you notice we have two extra fields in the node than the regular binary tree node. leftBit and rightBit. Let's see what these fields represent.
| leftBit=0 | left reference points to the inorder predecessor |
| leftBit=1 | left reference points to the left child |
| rightBit=0 | right reference points to the inorder successor |
| righBit=1 | right reference points to the right child |
Let's see why we need these fields and why we need a dummy node when If we try to convert the normal binary tree to a threaded binary
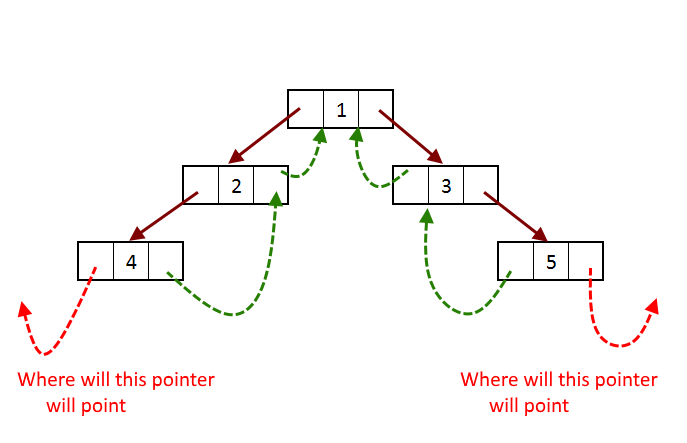
Now if you see the picture above, there are two references left most reference and right-most reference pointers has nowhere to point to.
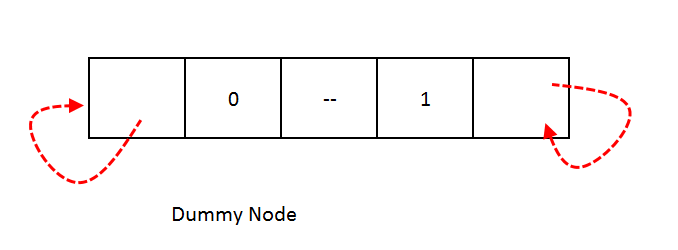
Need of a Dummy Node: As we saw that references left most reference and rightmost reference pointers have nowhere to point to so we need a dummy node and this node will always present even when the tree is empty.
In this dummy node, we will put rightBit = 1 and its right child will point to itself and leftBit = 0, so we will construct the threaded tree as the left child of the dummy node.
Let's see what the dummy node will look like:
Now we will see how this dummy node will solve our problem of references left most reference and right most reference pointers has nowhere to point to.
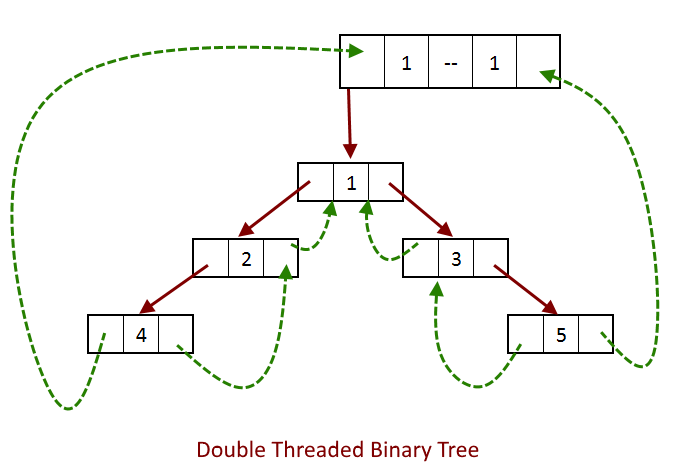
Now we will see the same operations in a double-threaded binary tree.
Insert():
The insert operation will be quite similar to Insert operation in Binary search tree with few modifications.
- To insert a node our first task is to find the place to insert the node.
- First, check if the tree is empty, which means the tree has just a dummy node then insert the new node into the left subtree of the dummy node.
- If the tree is not empty then find the place to insert the node, just like in normal BST.
- If the new node is smaller than or equal to the current node then check if leftBit =0, if yes then we have found the place to insert the node, it will be on the left of the subtree and if leftBit=1 then go left.
- If the new node is greater than the current node then check if rightBit =0, if yes then we have found the place to insert the node, it will be in the right of the subtree and if rightBit=1 then go right.
- Repeat steps 4 and 5 till the place to be inserted is not found.
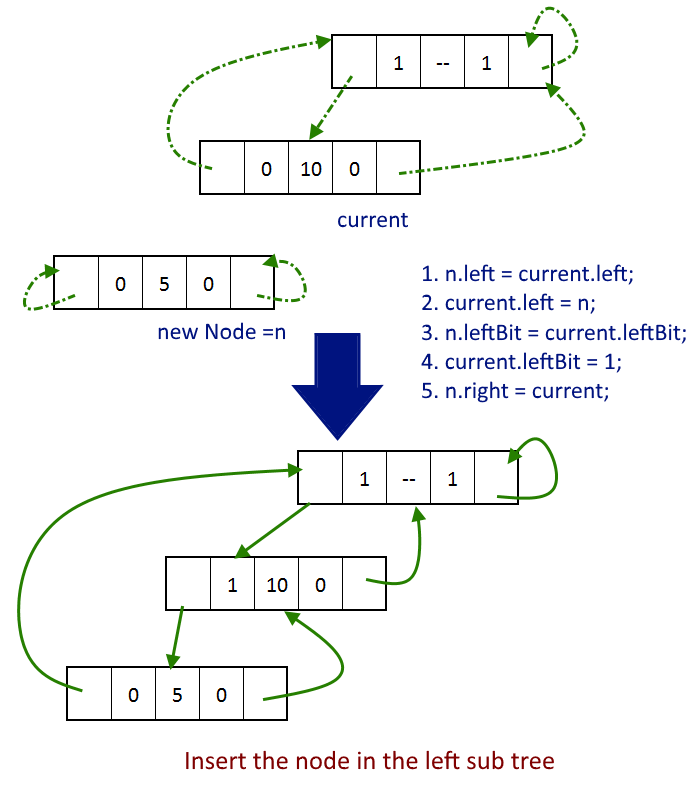
- Once decided where the node will be inserted, the next task would be to insert the node. first, we will see how the node will be inserted as the left child.
n.left = current.left; current.left = n; n.leftBit = current.leftBit; current.leftBit = 1; n.right = current;
see the image below for better understanding
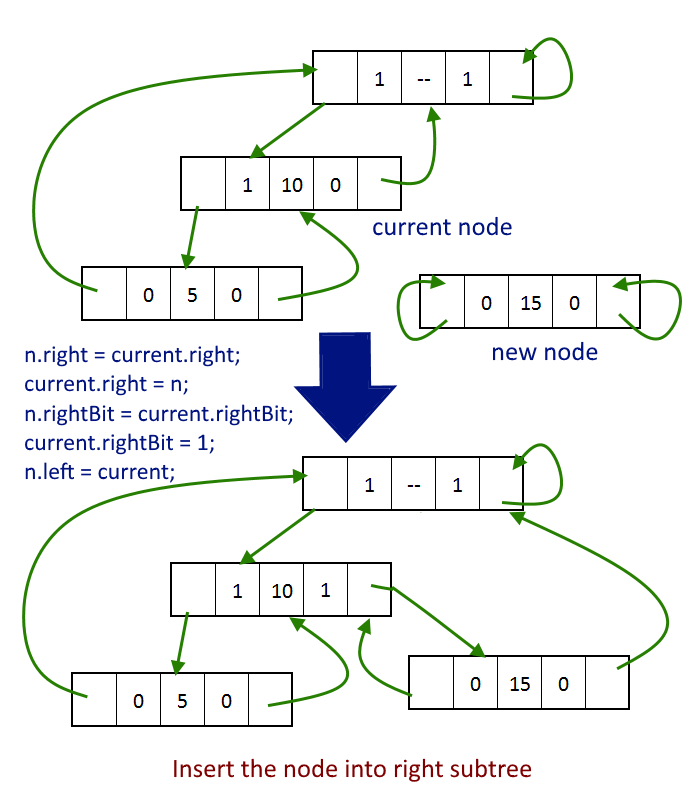
- To insert the node as the right child.
n.right = current.right; current.right = n; n.rightBit = current.rightBit; current.rightBit = 1; n.left = current;
see the image below for a better understanding.
Traverse():
Now we will see how to traverse in the double-threaded binary tree, we do not need a recursion to do that which means it won't require a stack, it will be done n one single traversal in O(n).
Starting from the left-most node in the tree, keep traversing the in-order successor and print it. (click here to read more about inorder successor in a tree).
See the image below for more understanding.
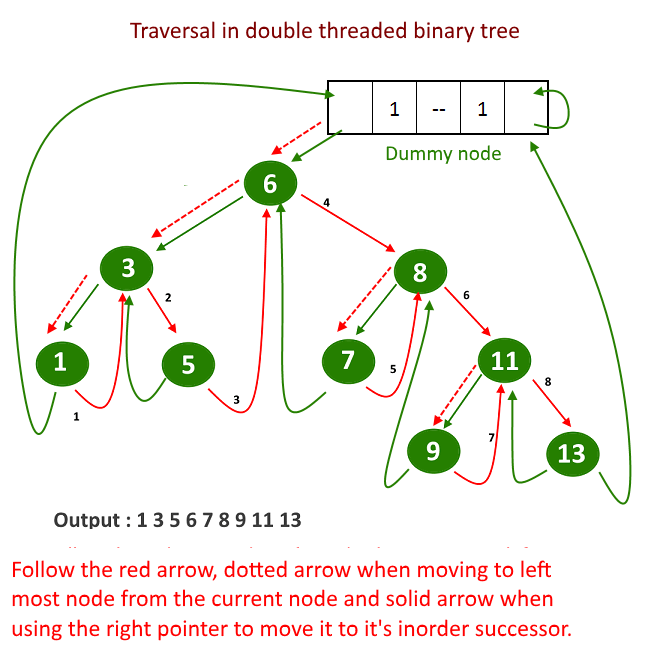
Output:
1 2 4 10 12 13 15

