|
This post is completed by 1 user
|
Add to List |
202. Dynamic Programming - Box Stacking Problem
Objective: You are given a set of n types of rectangular 3-D boxes, where the i^th box has height h(i), width w(i), and depth d(i) (all real numbers). You want to create a stack of boxes that is as tall as possible, but you can only stack a box on top of another box if the dimensions of the 2-D base of the lower box are each strictly larger than those of the 2-D base of the higher box. Of course, you can rotate a box so that any side functions as its base. It is also allowable to use multiple instances of the same type of box.
Source: http://people.csail.mit.edu/bdean/6.046/dp/ ,
Approach:
So we have n boxes. the first thing we will concentrate on is box rotations since each rotation will create more possibilities for making stacks, remember we have an unlimited number of boxes.
Box Rotations:
Though we say that we can rotate a box but if you look closely we have one 3 unique possibilities which will have different base areas.
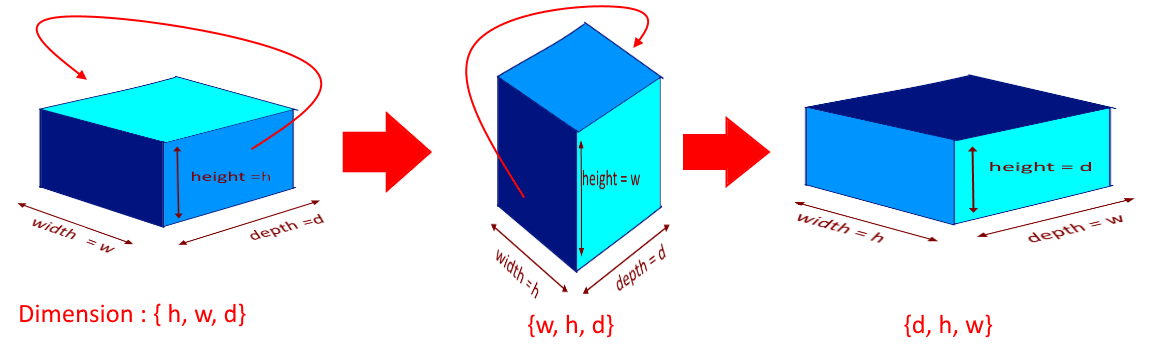
So for each given box, we will generate all the possibilities. Since we have unlimited boxes we will use all the boxes to make the stack of maximum height.
Now this problem has reduced to the variation of Longest Increasing Subsequence.
Now to create the stack of maximum height we need to place the box with the max base area at the bottom and on top of that box with 2nd best base area and so on.
Sort the boxes in descending order based on their base area. (I have solved this problem in java so I have overridden the compareTo(). Click here to read more about how to sort java objects. )
Now we have all the boxes in sorted order. We will take one box at a time ( in descending order). A box can be placed on another box only when the upper box is strictly larger than the lower box means the width and depth of the upper box is greater than the lower box.
Let's say
optHeight[i] = Maximum stack height created by i boxes.
For every box, we have two options either it can be placed in one of the boxes if it is smaller than those boxes or start a new stack with that box. So we will be creating multiple stacks. At the end, we will return the height of the biggest stack.
Let's see how the recursive equation will look like

Output:
All possible combination of boxes after rotation 11 20 40 20 11 40 40 11 20 5 8 9 4 7 9 8 5 9 9 5 8 7 4 9 9 4 7 1 2 3 2 1 3 3 1 2 Max height which can be obtained :78

