|
This post is completed by 2 users
|
Add to List |
169. Dynamic Programming - Coin Change Problem
Objective: Given a set of coins and amount, Write an algorithm to find out how many ways we can make the change of the amount using the coins given.
This is another problem in which i will show you the advantage of Dynamic programming over recursion.
Example:
Amount = 5
coins [] = {1,2,3}
Ways to make change = 5
{1,1,1,1,1} {1,1,1,2}, {1,2,2}, {1,1,3} {2,3}
Approach:
Recursive Solution:
- We can solve it using recursion.
- For every coin, we have an option to include it in the solution or exclude it.
- See the Code
Time Complexity : 2n
I have been asked by many readers how the complexity is 2^n. So including a simple explanation-
For every coin, we have 2 options, either we include it or exclude it so if we think in terms of binary, its 0(exclude) or 1(include). so for example, if we have 2 coins, options will be 00, 01, 10, and 11. so it's 2^2. for n coins, it will be 2^n. In all these options we will be checking whether that selection has made the change that is required.
But if we notice that we are solving many sub-problems repeatedly.
We can do better by applying Dynamic programming.
Dynamic Programming: Bottom-up -
Earlier we have seen "Minimum Coin Change Problem". This problem is slightly different than that but the approach will be a bit similar.
Create a solution matrix. (solution[coins+1][amount+1]).
Base Cases:
- if amount=0 then just return the empty set to make the change, so 1 way to make the change.
- if no coins are given, 0 ways to change the amount.
Rest of the cases:
- For every coin, we have an option to include it in the solution or exclude it.
- check if the coin value is less than or equal to the amount needed, if yes then we will find ways by including that coin and excluding the coin.
- Include the coin: reduce the amount by the coin value and use the sub-problem solution (amount-v[i]).
- Exclude the coin: solution for the same amount without considering that coin.
- If the coin value is greater than the amount then we can't consider that coin, so the solution will be without considering that coin.
Equation:
solution[coins+1][amount+1]
| = | 0 | if i=0 | |
| solution[i][j] | = | 1 | if j=0 |
| = | solution[i - 1][j] + solution[i][j - v[i - 1]] | if(coin[i]<=j) | |
| = | solution[i - 1][j]; | if(coin[i]>j) |
Example:
Amount = 5
coins [] = {1,2,3}
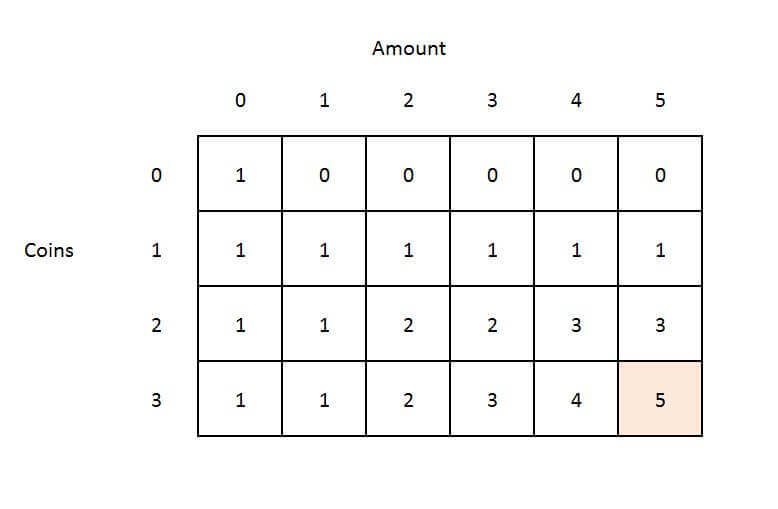
Output:
By Dynamic Programming 5

