|
This post is completed by 1 user
|
Add to List |
172. Dynamic Programming - Longest Common Substring
Objective: Given two string sequences write an algorithm to find, find the length of the longest substring present in both of them.
This problem has been asked in Amazon and Microsoft interviews. The approach to solving this problem will be slightly different than the approach in "Longest Common Subsequence"
What is the Longest Common Substring: The longest substring is a sequence that appears in the same order and is necessarily contiguous in both strings.
Example:
String A = "tutorialhorizon";
String B = "dynamictutorialProgramming";
Output: Length of Longest Common Substring: 8 ("tutorial").
Naive Approach:
Check all the substrings from the first string with the second string and keep track of the maximum.
Time Complexity: O(n2*m), O(n2) for the substring, and O(m) for checking all the substrings with the second string.
Better Solution: Dynamic Programming-
Earlier we have seen how to find "Longest Common Subsequence" in two given strings. The approach in this problem will be quite similar to that.
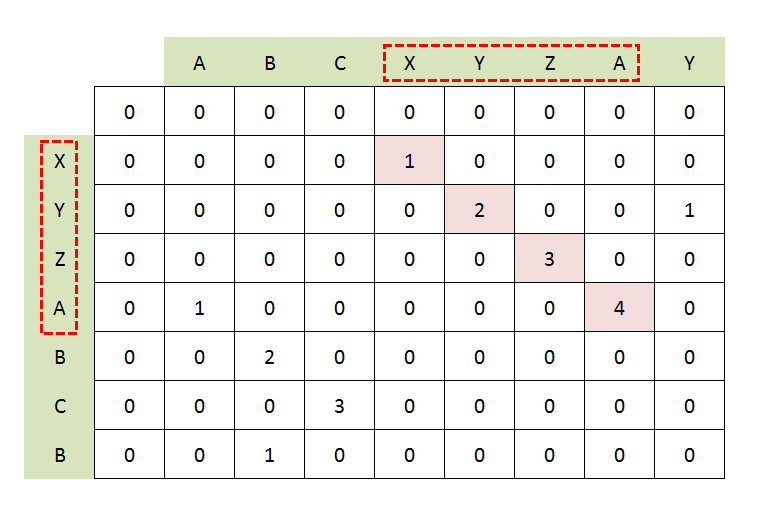
we will solve this problem in bottom-up manner. Create a matrix of the size of m*n and store the solutions of substrings to use later.
Base Cases: If any of the string is null then LCS will be 0. Check if ith character in one string A is equal to jth character in string B Case 1: both characters are the same LCS[i][j] = 1 + LCS[i-1][j-1] (add 1 to the result and remove the last character from both the strings and check the result for the smaller string.) Case 2: both characters are not the same. LCS[i][j] = 0
At the end, traverse the matrix and find the maximum element in it, This will be the length of the Longest Common Substring.
See the code for a better explanation.
LCS length: 8
Click here to see code for Top-down approach of same problem

