|
This post is completed by 1 user
|
Add to List |
244. Dynamic programming - Remove Boxes Problem | leetcode
Objective: Given a number of boxes with different colors represented by different positive numbers. You need to remove all the boxes in several rounds, each time you can choose continuous boxes with the same color (means with the same numbers, composed of k boxes, k >= 1), remove them, and get k*k points.
Write an algorithm to get the maximum points by removing all the boxes.
Reference: https://leetcode.com/problems/remove-boxes/description/
Example
1233211 Remove 33 – Profit = 2*2 = 4, Remaining = 12211 Remove 22 – Profit = 4 + 2*2 = 8, Remaining = 111 Remove 11 - Profit = 3*3 + 8 = 17
We will try to club identical numbers so that when we will remove those together, will get the maximum profit since if we are removing x boxes then the profit will be x*x.
Approach:
Recursion:
- Will try every option and choose the best one.
- Start from index 0, pick the maximum identical numbers possible, add the profit and solve the rest of the string using recursion.
- Leave the option chosen in step 2 and follow the same approach taken in step 2. Solve the remaining string (which includes the option from step 2) recursively.
- Pick the maximum among results from steps 2 and step 3.
See the diagram below for more understanding.
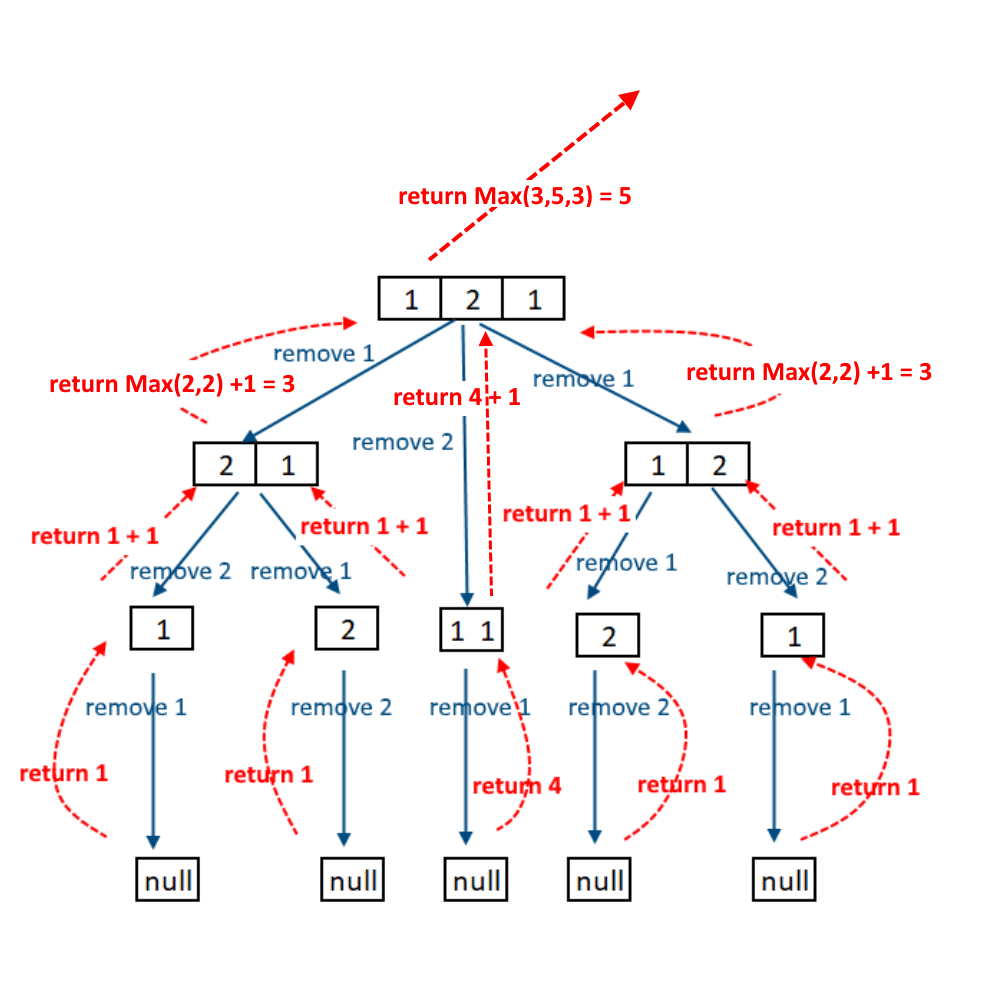
Time Complexity: 2n.
If we look closely at the diagram above we are solving many sub-problems recursively. Here we will use Top-down approach of dynamic programming. We will use Hash Map to store the results of the subproblems and whenever we make a recursive call, first check if the subproblem is already solved, if yes then use it.
Output:
Max Profit: 12
Time taken: 0 seconds

