|
This post is completed by 2 users
|
Add to List |
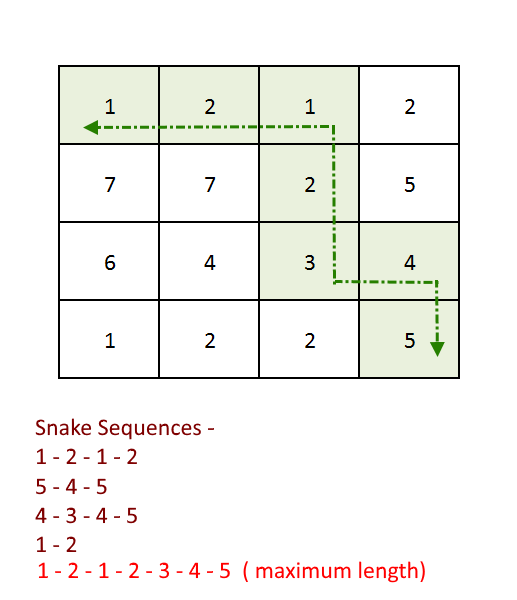
209. Find longest Snake sequence in a given matrix
Objective: Given a two-dimensional matrix, write an algorithm to find out the snake sequence which has the maximum length. There could be many snake sequences in the matrix, you need to return the one with the maximum length. Travel is allowed only in two directions, either go right OR go down.
What is snake sequence: A snake sequence can be made if the number in the adjacent right cell or the number in the adjacent down cell is either +1 or -1 from the number in the current cell.
Example:
Approach:
- This problem is the extension of the problem "Count all paths from top left to bottom right of a mXn matrix" with some extra conditions.
- You can travel only in two directions, either go right or go down.
- All we need to take care of is one extra condition that we can travel only to the adjacent cells (right or down) only if the number in those cells has a difference of 1 from the current cell.
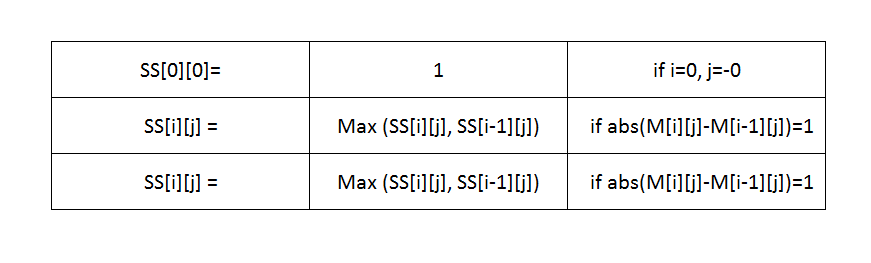
- Have a temporary storage, two-dimensional array to store the results of the snake result.
- Keep tracking of maximum length and at the end print the sequence using a temporary array.
- We will use the Bottom-up approach of Dynamic programming and store the results of sub problems to reuse them in the future.
- See the recursive equation and code for a better understanding.
Output:
Max Snake Sequence : 7 - 5 - 4 - 3 - 2 - 1 - 2 - 1

