|
This post is completed by 1 user
|
Add to List |
338. Find Number of reverse pairs in an array
Objective: Given an array of integers A[],find no of reverse pairs means no of (i, j) pairs where i < j and A[i]>A[j].
This problem is also asked as Count Inversions in an array.
Example:
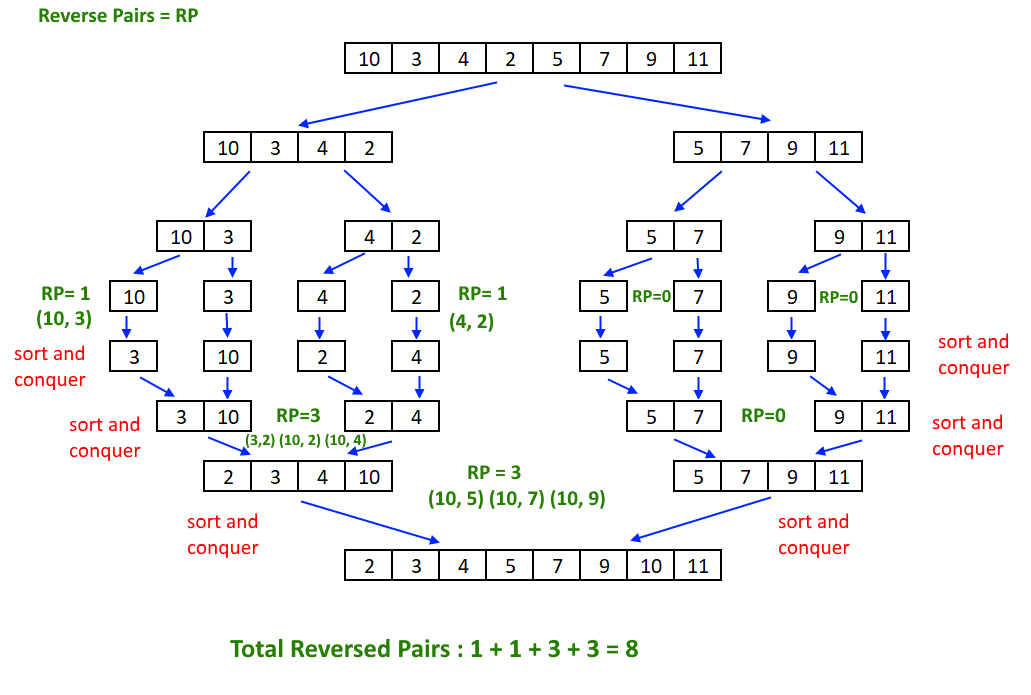
A[] = {10,
3, 4, 2, 5, 7, 9, 11}
Output:7
Reversed pairs: (10, 3) (10, 4) (10, 2) (10, 5) (10, 7) (10, 9) (3, 2) (4, 2) = 8
Approach:
Naïve Approach:
Use nested for loops and compare each element with all other elements in array and check if it is reversed pair, if yes then add it to the result. At the end print the result.
Time Complexity: O(N2)
Better Approach: Divide and Conquer
Earlier we have seen a similar problem where the array is sorted in two parts and we solved it O(N) time. We recommend reading the following article before continue.
Steps:
- Divide the array into 2 parts.
- Sort both the parts.
- Find reverse pairs in both parts, add them to result and then merge both the parts. (This step is important, make sure you find the reverse pairs first before you sort them because sorting will change the order).
- We can find the reverse pairs in O(N)time as we have done in this article - Find number of reverse pairs in an array sorted in two parts.
- You might think that sorting will change the order of the array then the result will be wrong for finding reverse pairs but here the trick is we are finding the reverse pairs before we sort let’s take one example.
Example:
{10, 3, 4, 2}
Divide –
{10, 3} and {4, 2}
Divide –
{10} {3} {4} {4}
find the reverse pair in {10} {3} arrays
Reverse pair
= (10, 3) , now sort it then merge it, new array will be {3, 10}
find the reverse pair in {4} {2} arrays
Reverse pair
= (4, 2) , now sort it then merge it, new array will be {2, 4}
find the reverse pair in {3, 10} {2, 4} arrays –Now if you notice order of 3, 10 is changed but still, it will not affect the result since pair (10, 3) is already found and further pairs which we will find for them 10 and 3 will be on the left side.
See the image below for full-example -