|
This post is completed by 1 user
|
Add to List |
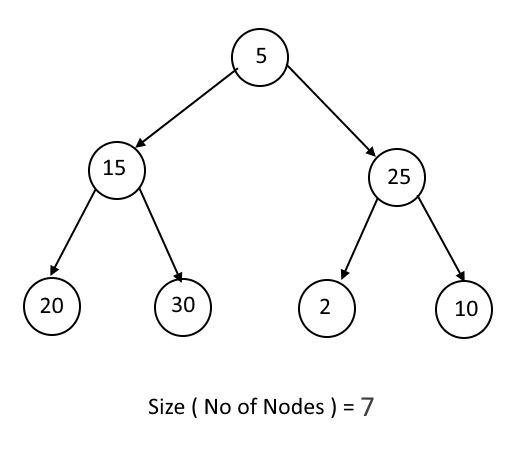
176. Find the Size of a Binary Tree without Recursion
Objective: Given a binary tree, Write a non-recursive algorithm to find the size of the tree.
Note : Size of the tree is number of nodes in the tree
In our earlier post (link) we have seen the clean and simple recursive approach for finding the size of the tree. Now we will see how to solve it without recursion.
If we are not using recursion then we need a data structure to store the tree traversal, we will use queue here.
Solution is exactly similar to tree traversal without recursion. Just that we will keep counting the number of nodes.
Output:
Tree Size: 5