Given a binary tree, find out the maximum sum of value from root to each leaf.
Objective: – Find the maximum sum leaf to root path in a Binary Tree. Means in all the paths from root to leaves, find the path which has the maximum sum.
Input: A binary tree
Example:
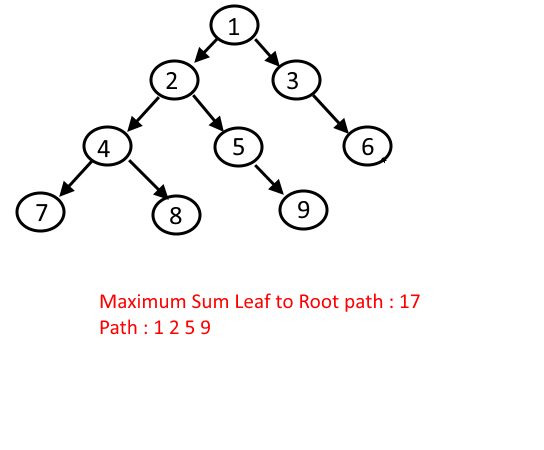
Approach:
This solution will be divided into two parts
Find the leaf which has the maximum sum from root.
- Take a global variable maxLeaf and maxSum. (this maxLeaf will the node which has the maximum sum path and maxSum will the maximum sum.)
- Do the preorder traversal
- At each node, maintain a another variable sum = sum + root.data.
- When ever you reach to any leaf, check if sum>maxSum, if yes then update the maxLeaf and maxSum.
Print the path from root to that leaf.
Please refer this link to print the path.
Complete Code:
Output:
Maximum Sum Leaf to Root path :18 Path : 8 6 3 1
