Given a binary tree, Find the Maximum Path Sum between Any Two Leaves

Objective: Given a binary tree, Find the maximum path sum from one leaf node to another.

Input: A binary tree.

Example:

Maximum Sum path between two leaves

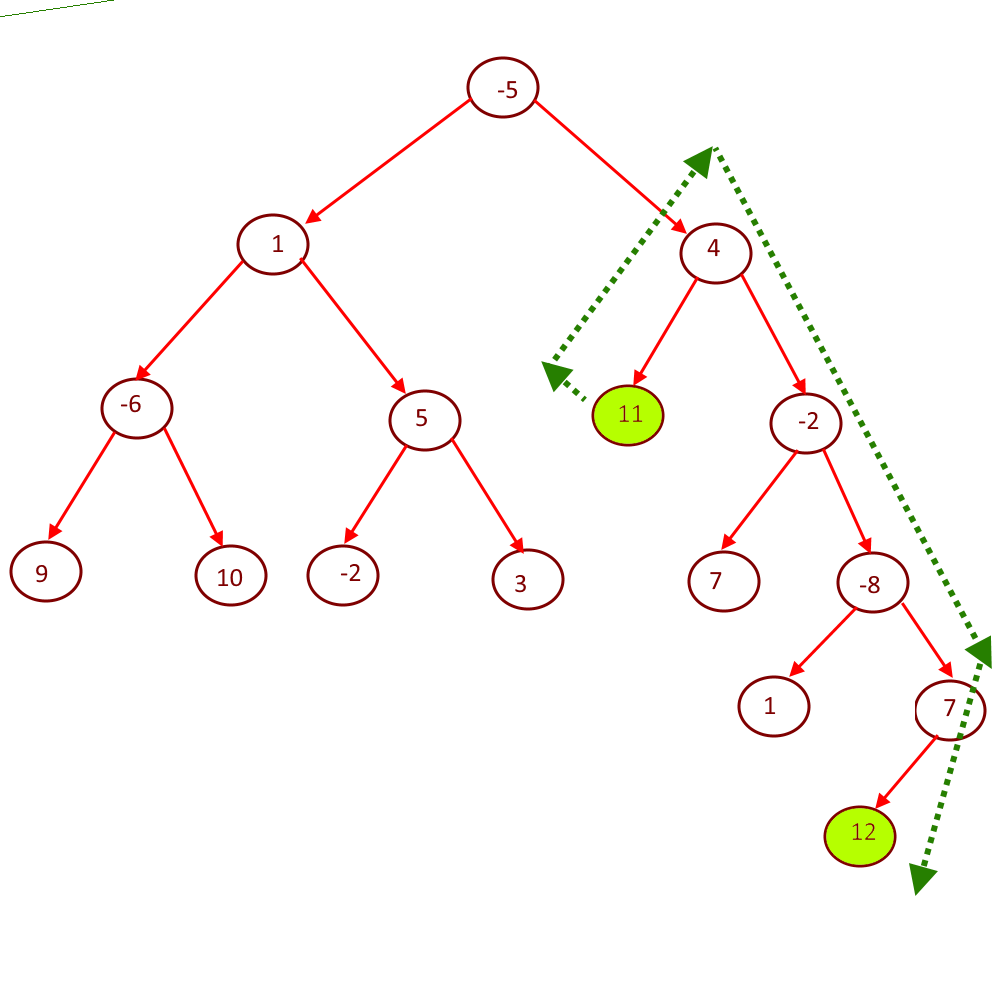
Approach:

• Now we will calculate the max path sum between two leaves node
• So our max path will be either on the left sub tree OR
• Our max path will be either on the right sub tree OR
• Our max path will have some part in left and some part in right and passes through through the root
• Take a variable say, “maxSoFar=0” this will our final result.
• Do postOrder traversal, This will give you result from left and right subtree
• Now at each node calcuate sumCurrent =Max of (result of leftSubtree,result of RightSubtree, result of leftSubtree+result of RightSubtree + Root data)
• if(maxSoFar<sumCurrent) then maxSoFar = sumCurrent
• At each node return max(result of leftSubtree,result of RightSubtree)+root.data;
• See Picture

Complete Code:Run This Code

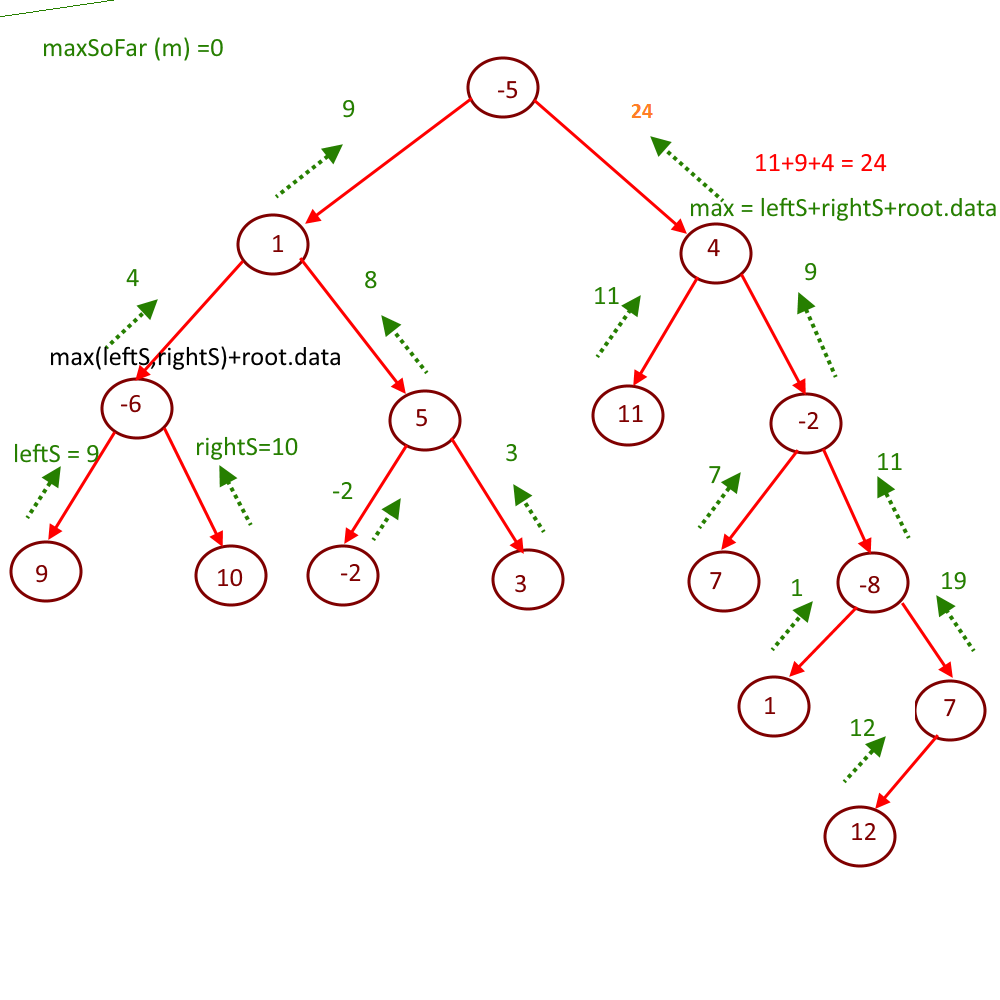
Output:

Max Path Sum Between Two Leaves is 24