|
Be the first user to complete this post
|
Add to List |
275. Graph – Detect Cycle in a Directed Graph using colors
Objective: Given a directed graph write an algorithm to find out whether graph contains cycle or not.
Example:
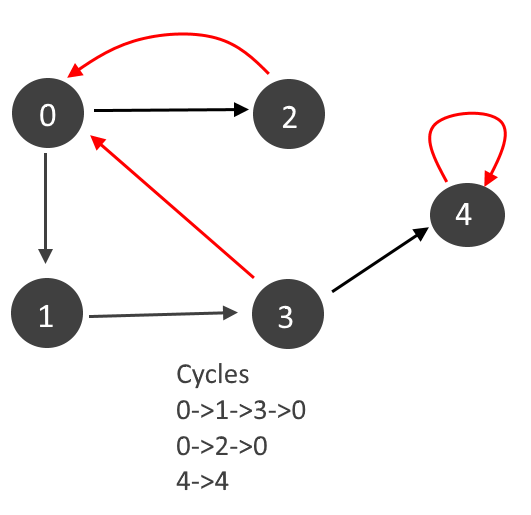
Approach:
Graph contains cycle if there are any back edges. There are two types of back edges as seen in the example above (marked in red)
- Edge from a vertex to itself. Self loop. (4-4)
- Edge from any descendent back to vertex.
Earlier we have seen detect cycle using recursion stack. In this article we will how to use colors to detect cycle in graphs.
Using Colors:
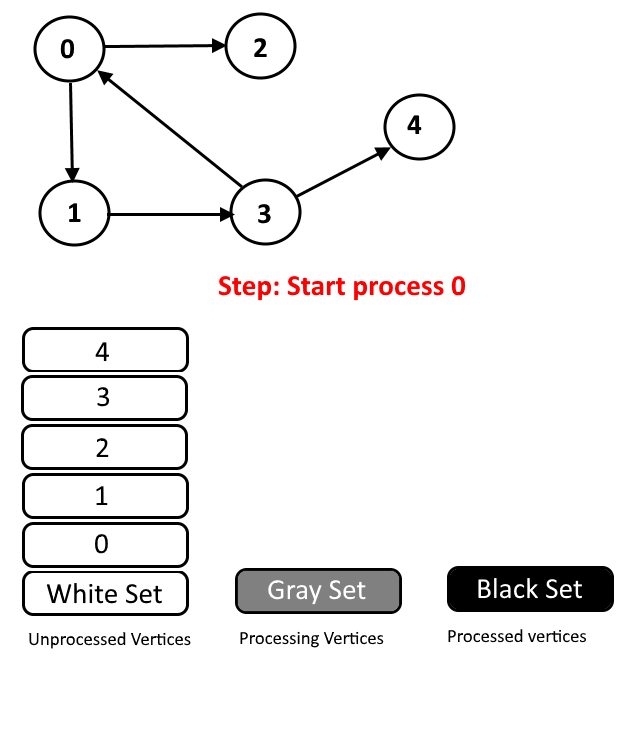
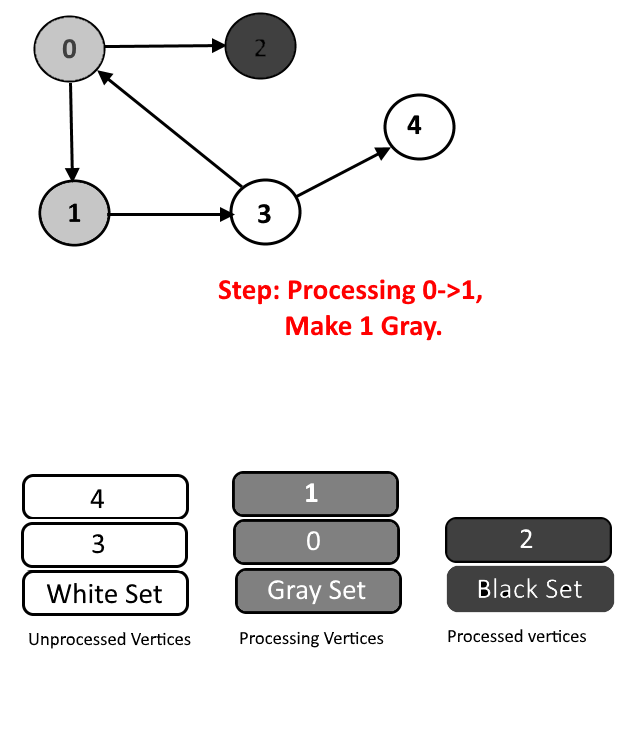
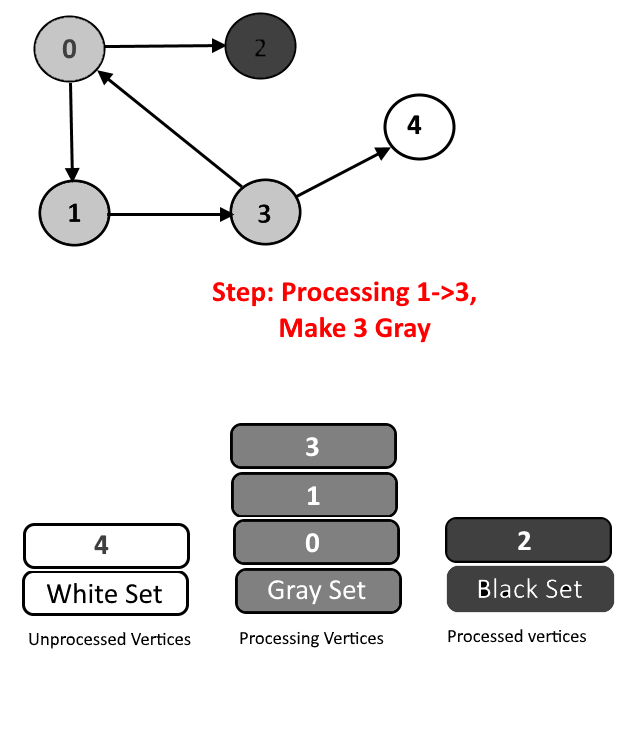
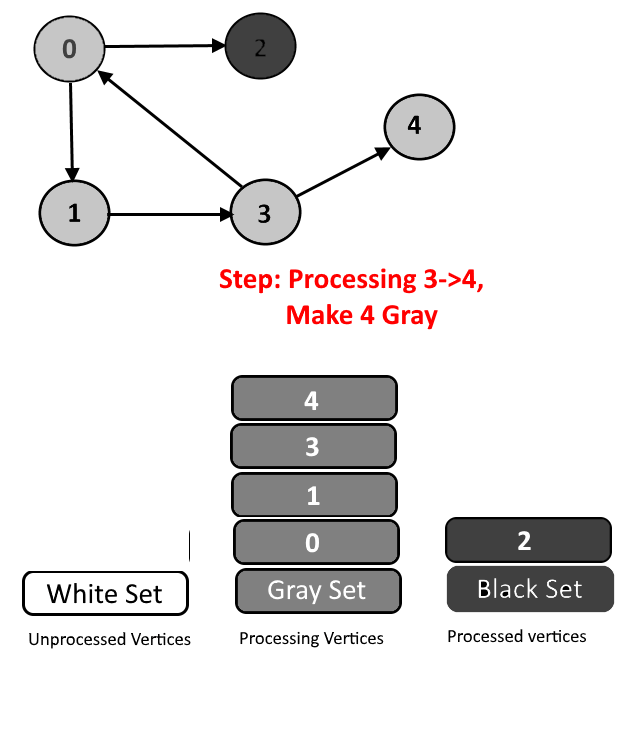
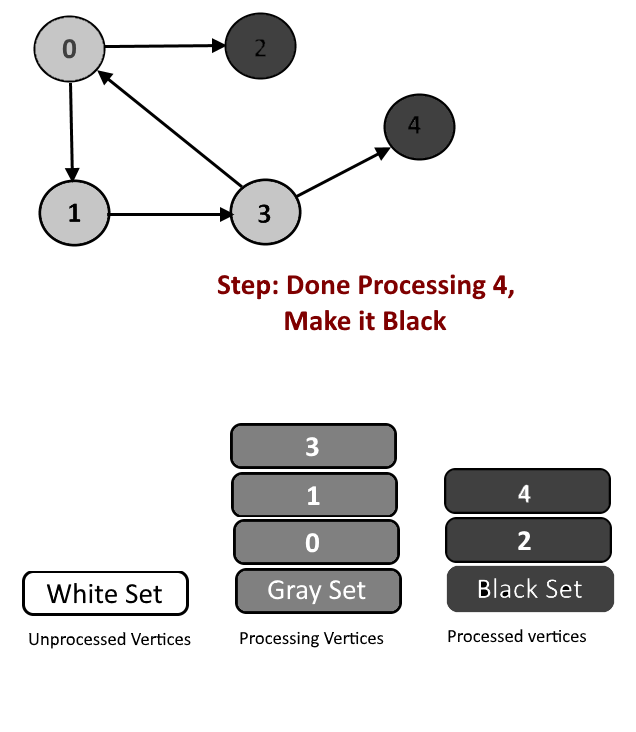
We will assign every vertex a color and will use 3 colors- white, gray and black.
- White Color: Vertices which are not processed will be assigned white colors. So at the beginning all the vertices will be white.
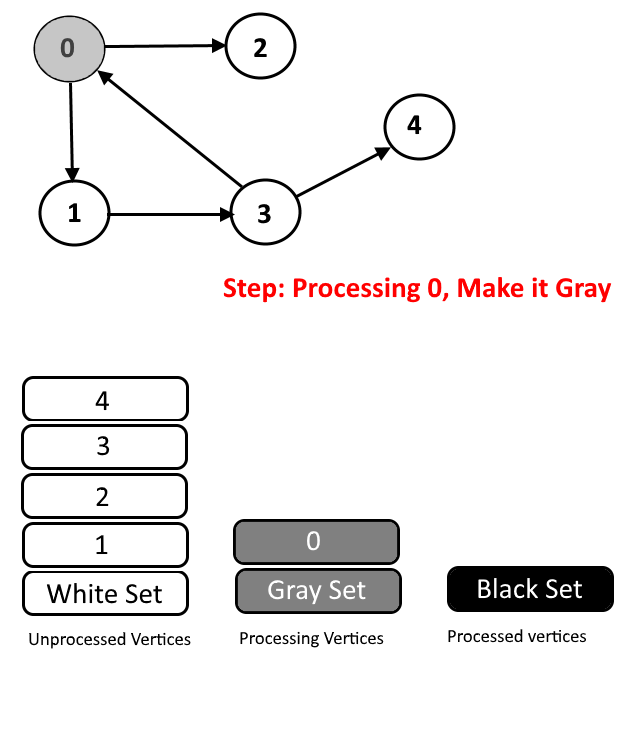
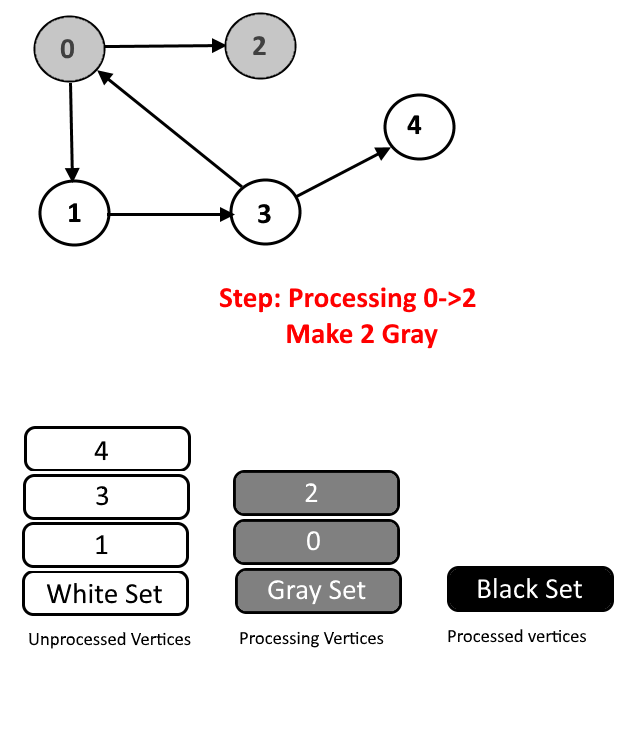
- Gray Color: Vertices will are currently being processed. If DFS(Depth-First Search) is started from a particular vertex will be in gray color till DFS is not completed (means all the descendants in DFS are not processed.)
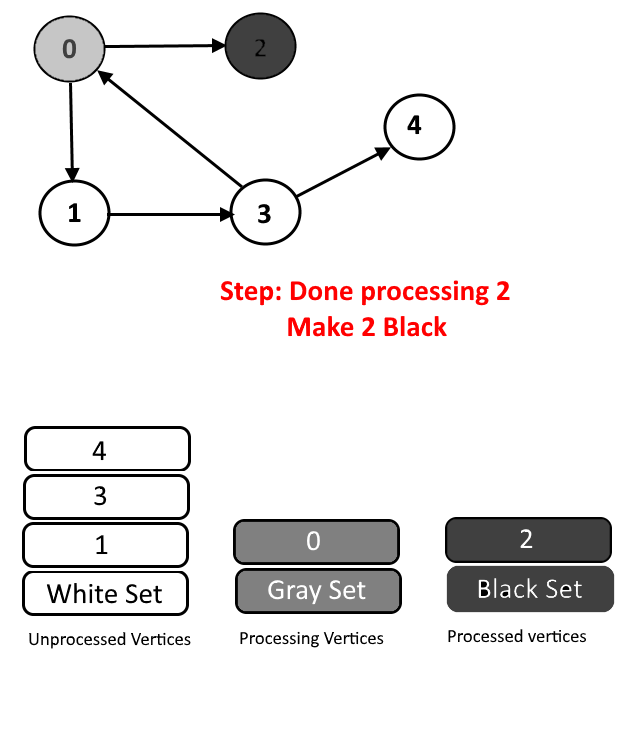
- Black Color: Vertices for which the DFS is completed, means all the processed vertices will be assigned black color.
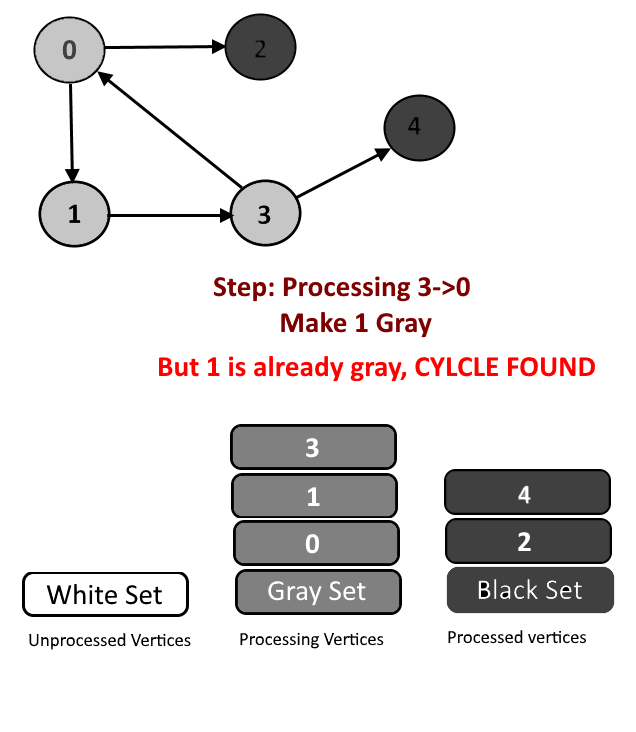
- Cycle Detection: During DFS if we encounter a vertex which is already in Gray color (means this vertex already in processing and in Gray color in the current DFS) then we have detected a Cycle and edge from current vertex to gray vertex will a back edge.
- Example – Graph 2->3->4->2. Start DFS from vertex 2 (make it gray). Then vertex 3 and 4 will be in processing (Gray color) and when 4->2 will be in processing, vertex 2 needs to be colored in gray but vertex 2 is already in gray color, means cycle is detected.
See the animation below for more understanding.
Output:
is Cycle present: true