|
This post is completed by 1 user
|
Add to List |
273. Graph – Detect Cycle in a Directed Graph
Objective: Given a directed graph write an algorithm to find out whether graph contains cycle or not.
Example:
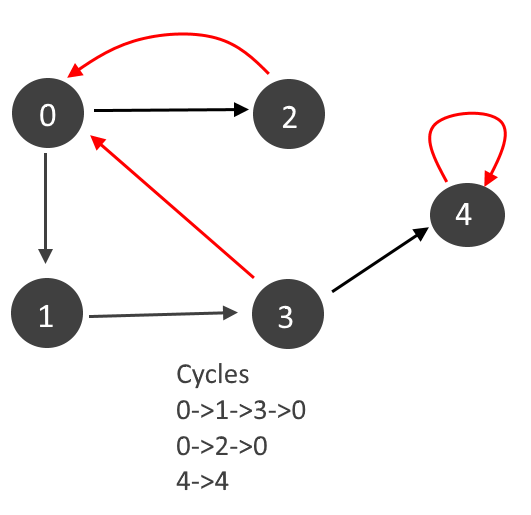
Approach:
Graph contains cycle if there are any back edges. There are two types of back edges as seen in the example above (marked in red)
- Edge from a vertex to itself. Self loop. (4-4)
- Edge from any descendent back to vertex.
Use DFS(Depth-First Search) to detect the back edge
- Do the DFS from each vertex
- For DFS from each vertex, keep track of visiting vertices in a recursion stack (array).
- If you encounter a vertex which already present in recursion stack then we have found a cycle.
- Use visited[] for DFS to keep track of already visited vertices.
How different is recursion stack[] from visitied [].
- Visited[] is used to keep track of already visited vertices during the DFS is never gets
- Recursion stack[] is used from keep track of visiting vertices during DFS from particular vertex and gets reset once cycle is not found from that vertex and will try DFS from other vertices.
- See the code from more understanding.
Time Complexity: O(V+E)
Output:
is Cycle present: True

