|
Be the first user to complete this post
|
Add to List |
280. Graph – Find Cycle in Undirected Graph using Disjoint Set (Union-Find)
Objective: Given a graph, check if the graph contains a cycle using a disjoint set.
Note: Disjoint-set data structure, also called a union–find data structure or merge–find set.
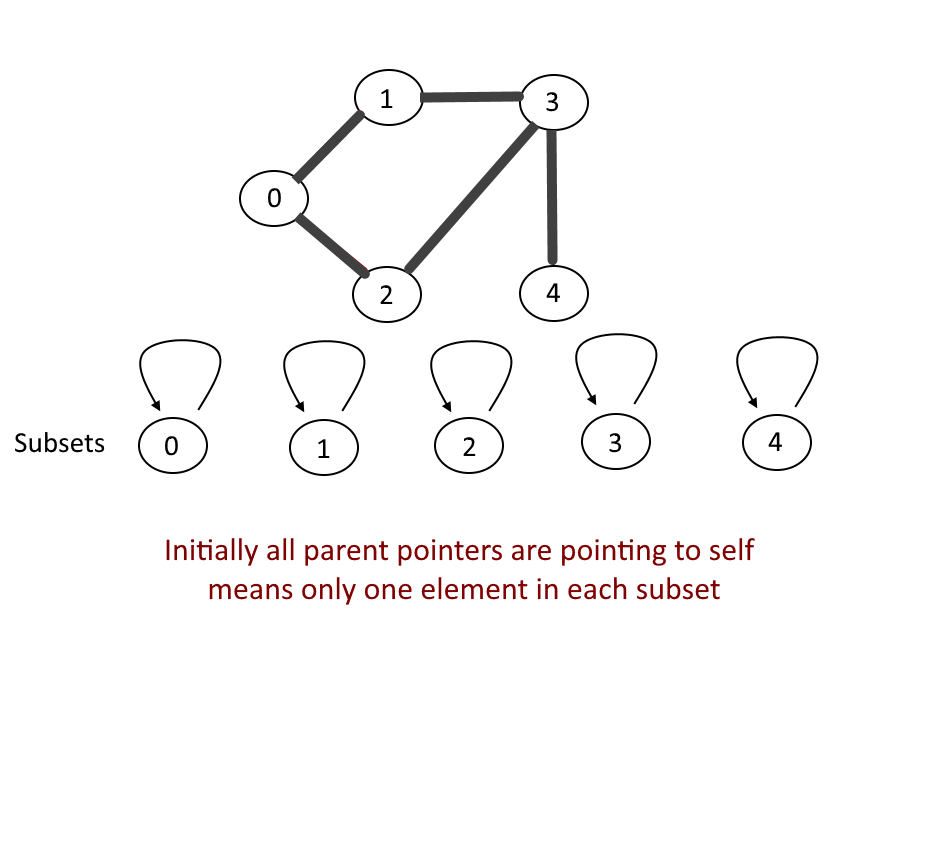
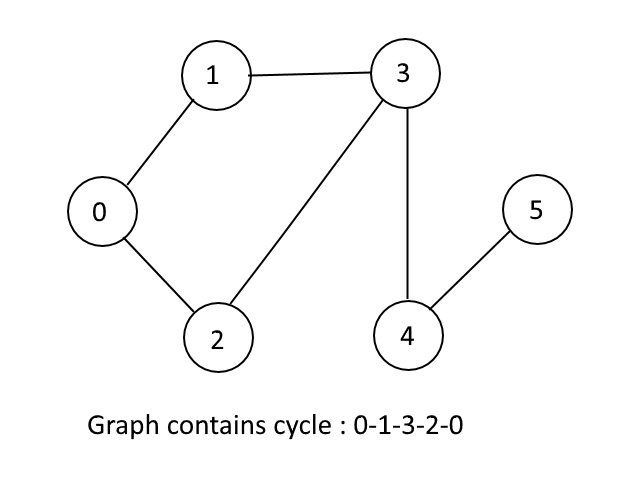
Example:
Earlier in Detect Cycle in Undirected Graph using DFS we discussed how to find cycles in graphs using DFS. In this article we will discuss how to find a cycle using a disjoint set.
It is strongly recommended to read “Disjoint-set data structure” before continue reading this article.
How to find the cycle:
- The makeset operation makes a new set by creating a new element with a parent pointer to itself.
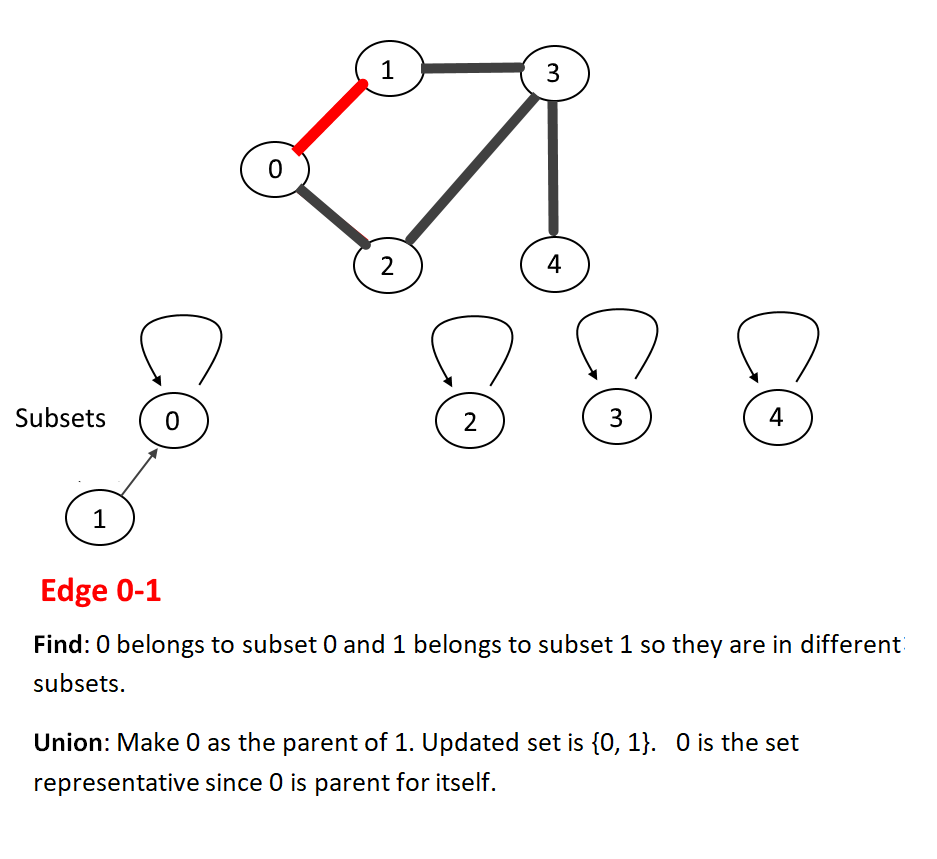
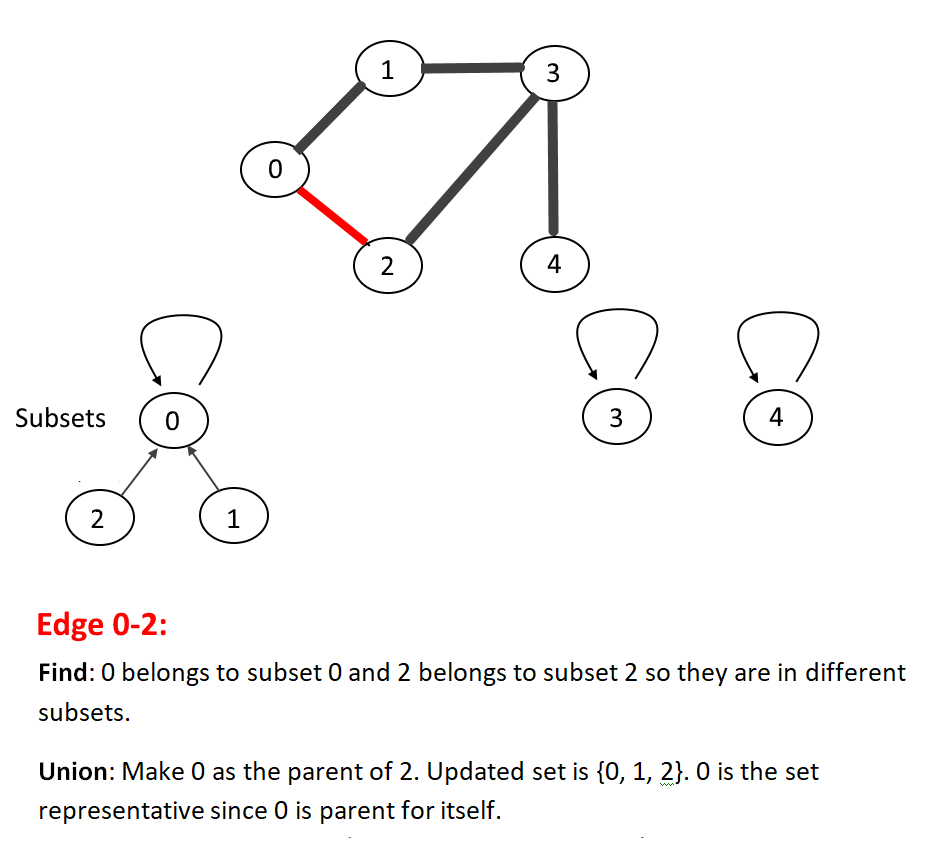
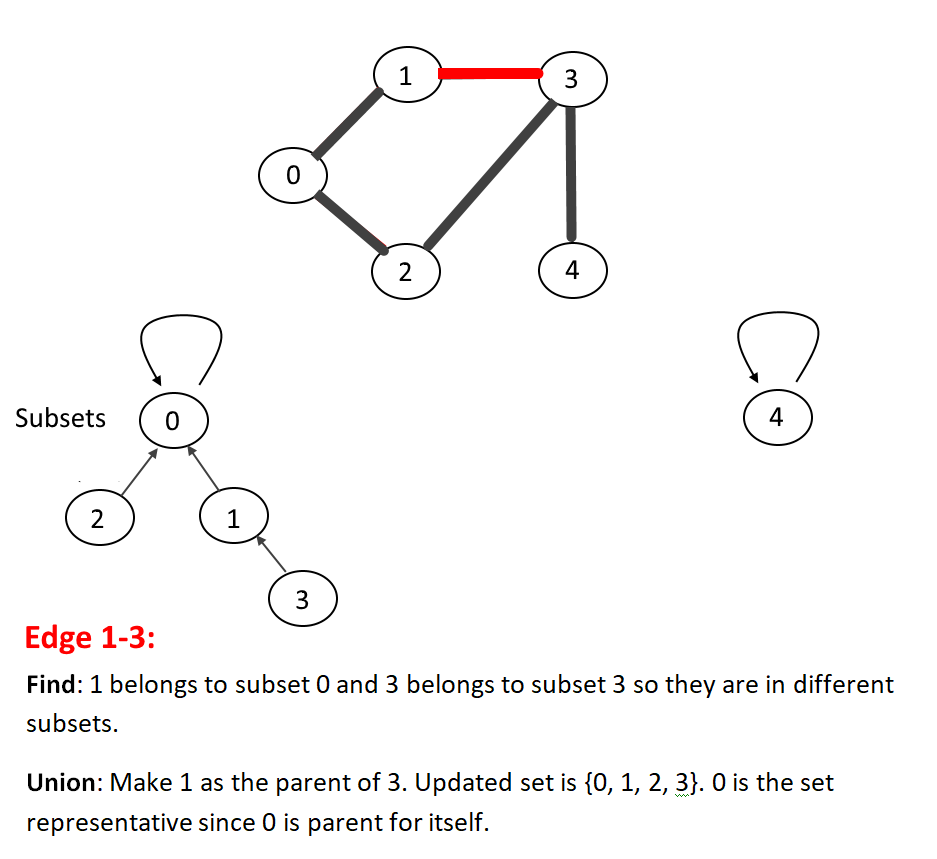
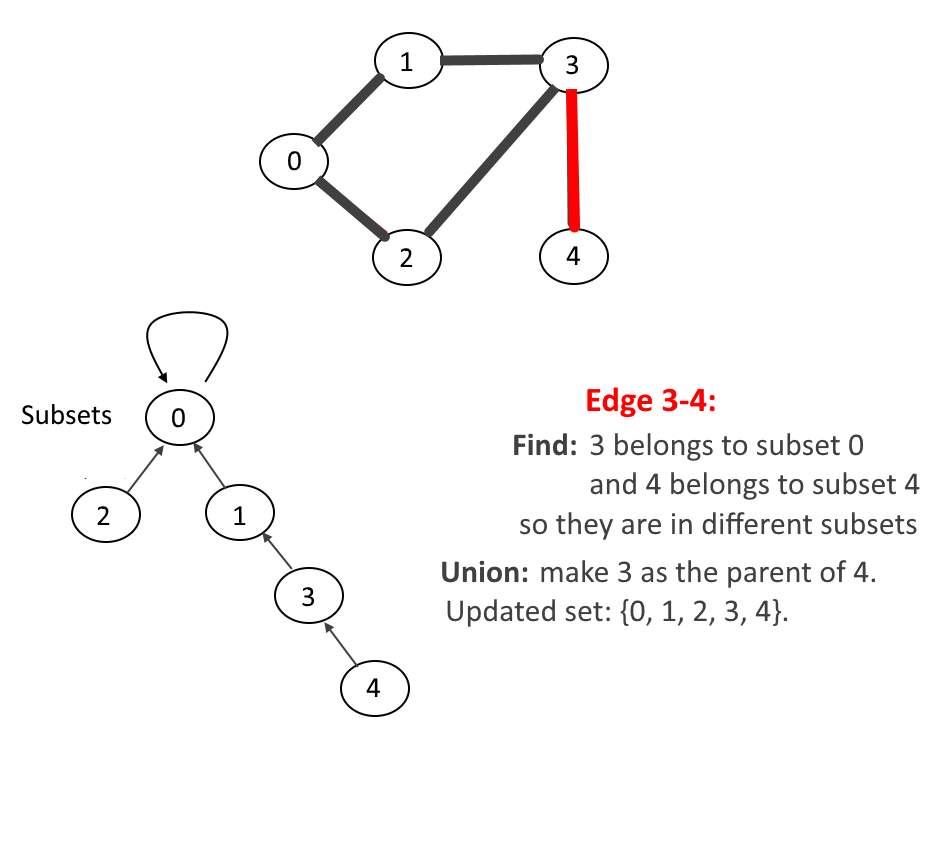
- Then process each edge of the graph and perform find and Union operations to make subsets using both vertices of the edge.
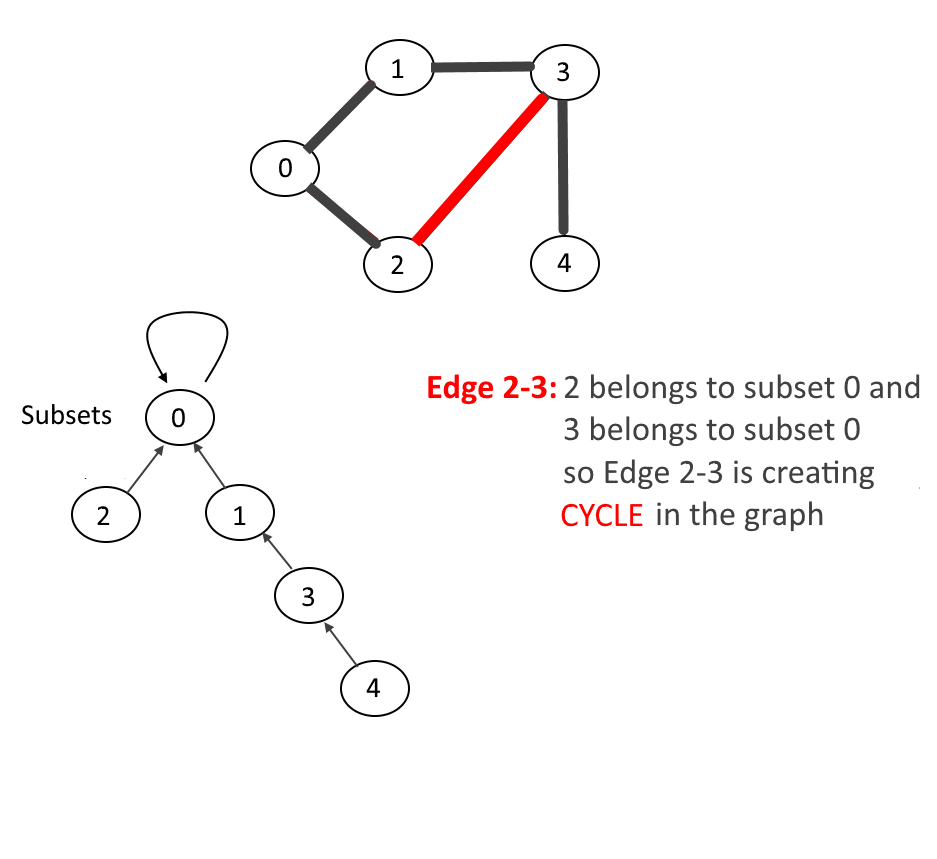
- If the find operation on both the vertices returns the same parent (which means both vertices belong to the same subset) then the cycle is detected.
Let's walk through one example for more understanding, see the animation below:
Output:
Graph contains cycle: true
Ref: wiki