|
This post is completed by 1 user
|
Add to List |
266. Graph Implementation – Adjacency Matrix | Set 3
Earlier we had discussed in Graph Representation – Adjacency Matrix and Adjacency List about Graph and its different representations and we read Graph Implementation – Adjacency List .In this article we will implement graph using adjacency matrix.
We would recommend to read the theory part of Graph Representation – Adjacency Matrix and Adjacency List before continue reading this article.
Let’s revise few basic concepts:
What is Graph:
G = (V,E)
Graph is a collection of nodes or vertices (V) and edges(E) between them. We can traverse these nodes using the edges. These edges might be weighted or non-weighted.
Adjacency Matrix:
Adjacency Matrix is 2-Dimensional Array which has the size VxV, where V are the number of vertices in the graph. See the example below, the Adjacency matrix for the graph shown above.
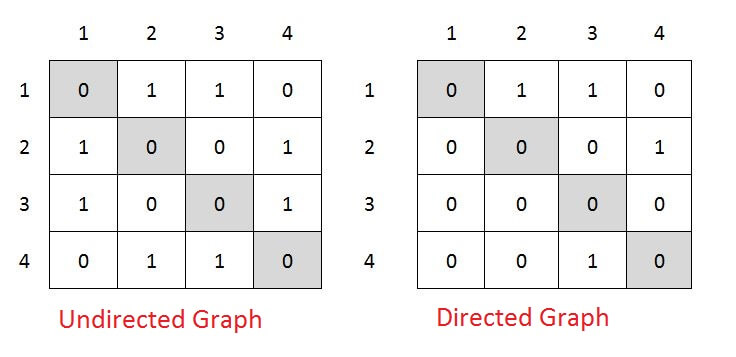
- adjMaxtrix[i][j] = 1 when there is edge between Vertex i and Vertex j, else 0.
- It’s easy to implement because removing and adding an edge takes only O(1) time.
- But the drawback is that it takes O(V2) space even though there are very less edges in the graph.
Output:
Graph: (Adjacency Matrix) 0 1 0 0 1 1 0 1 1 1 0 1 0 1 0 0 1 1 0 1 1 1 0 1 0 Vertex 0 is connected to:1 4 Vertex 1 is connected to:0 2 3 4 Vertex 2 is connected to:1 3 Vertex 3 is connected to:1 2 4 Vertex 4 is connected to:0 1 3

