|
This post is completed by 3 users
|
Add to List |
144. Introduction To Dynamic Programming - Fibonacci Series
What is Dynamic Programming:
Dynamic programming is a technique to solve the recursive problems in more efficient manner. Many times in recursion we solve the sub-problems repeatedly. In dynamic programming we store the solution of these sub-problems so that we do not have to solve them again, this is called Memoization.
Dynamic programming and memoization works together. So Most of the problems are solved with two components of dynamic programming (DP)-
- Recursion - Solve the sub-problems recursively
- Memoization - Store the solution of these sub-problems so that we do not have to solve them again
Example:
Fibonacci Series : The current number is the sum of previous two number. If can be defined as
Fibonacchi(N)
= 0 for n=0
= 1 for n=1
= Fibonacchi(N-1)+Finacchi(N-2) for n>1
Now we see the Recursion Solution:
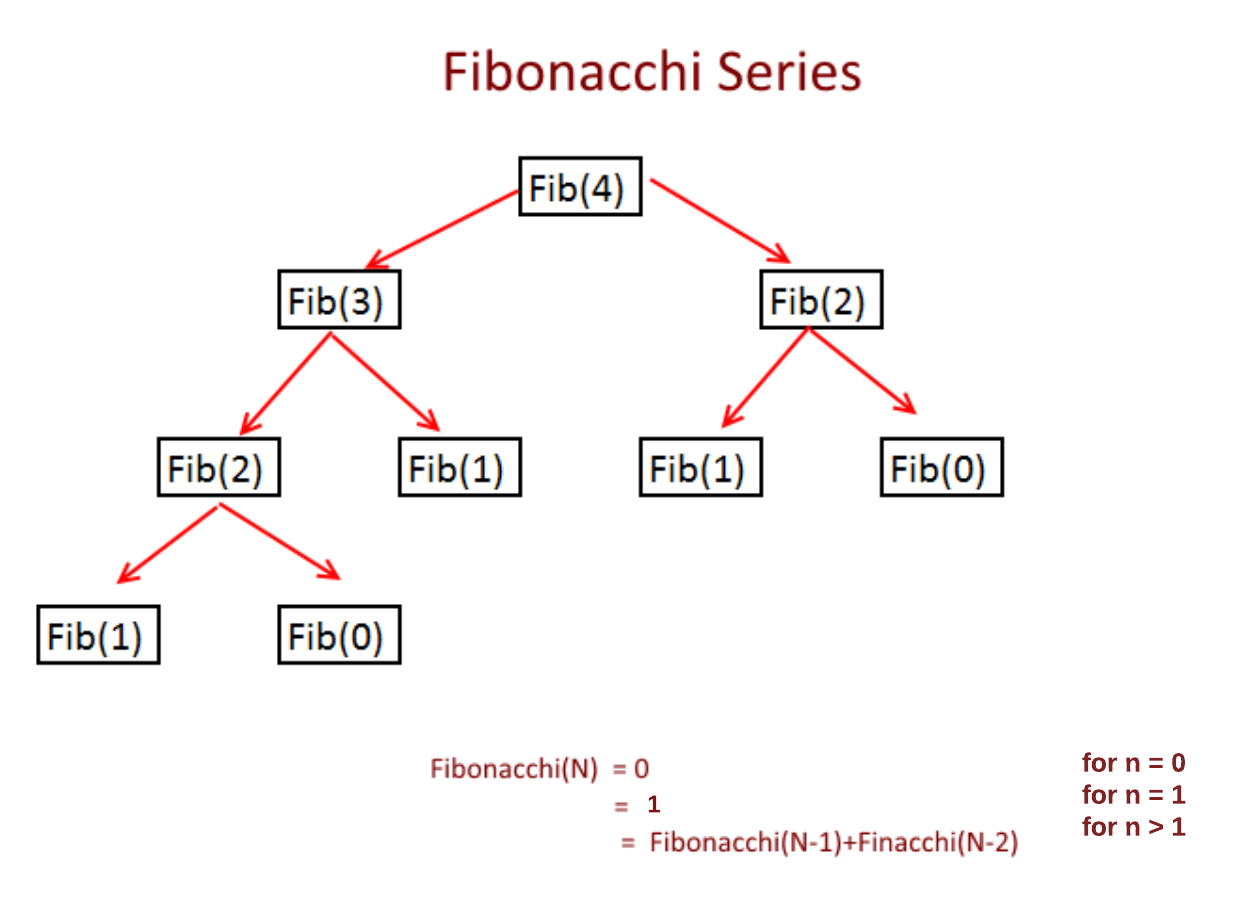
Now as you can see in the picture above while you are calculating Fibonacci(4) you need Fibonacci(3) and Fibonacci(2), Now for Fibonacci(3), you need Fibonacci (2) and Fibonacci (1) but you notice you have calculated Fibonacci(2) while calculating Fibonacci(4) and again calculating it. So we are solving many sub-problems again and again.
Time Complexity:
T(n) = T(n-1) + T(n-2) + 1 = 2n = O(2n)
Use Dynamic Programming - Memoization:
Store the sub-problems result so that you don't have to calculate again. So first check if solution is already available, if yes then use it else calculate and store it for future.
Time Complexity: O(n) , Space Complexity : O(n)
Two major properties of Dynamic programming-
To decide whether problem can be solved by applying Dynamic programming we check for two properties. If problem has these two properties then we can solve that problem using Dynamic programming.
- Overlapping Sub-problems
- Optimal Substructure.
Overlapping Sub-problems:
Overlapping sub-problems, as the name suggests the sub-problems needs to be solved again and again. In recursion we solve those problems every time and in dynamic programming we solve these sub problems only once and store it for future use. As we can see in the picture below that we are solving many sub-problems repeatedly.

Optimal Substructure: If a problem can be solved by using the solutions of the sub problems then we say that problem has a Optimal Substructure Property.
Dynamic Programming Approaches:
- Bottom-Up
- Top-Down
Bottom-Up Approach:
Suppose we need to solve the problem for N, We start solving the problem with the smallest possible inputs and store it for future. Now as you calculate for the bigger values use the stored solutions (solution for smaller problems).
Bottom-Up solution for Fibonacci Series:
Top-Down Approach:
Break the problem into sub-problems and solve them as needed and store the solution for future

