|
This post is completed by 1 user
|
Add to List |
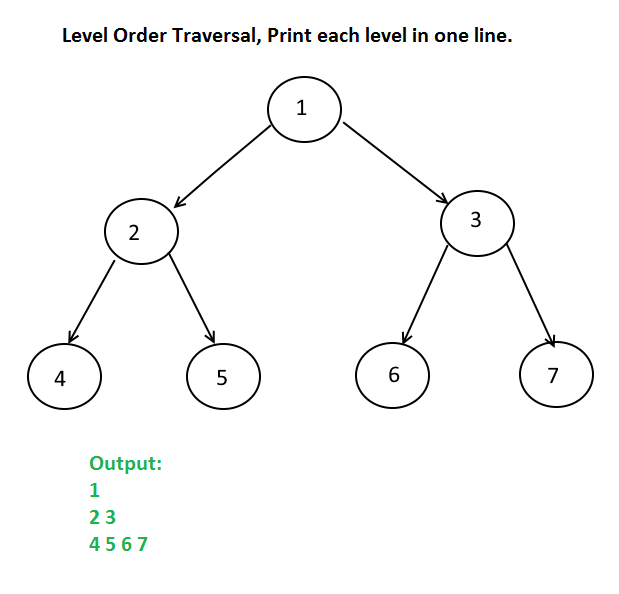
39. Level Order Traversal, Print each level in separate line
Objective: Given a Binary tree, Print each level of a tree in a separate line.
NOTE: This problem is very similar to Create Linked Lists of all the nodes at each depth
Example:
Approach:
Naive Approach:
- Get the height of the tree.
- Put a for loop for each level in the tree.
- for each level in step 2, do pre-order traversal and print only when the height matches the level.
- Look at the code for a better explanation
Time Complexity: O(N^2) - because at each level we are traversing the entire tree.
Better Solution: Time Complexity - O(N)
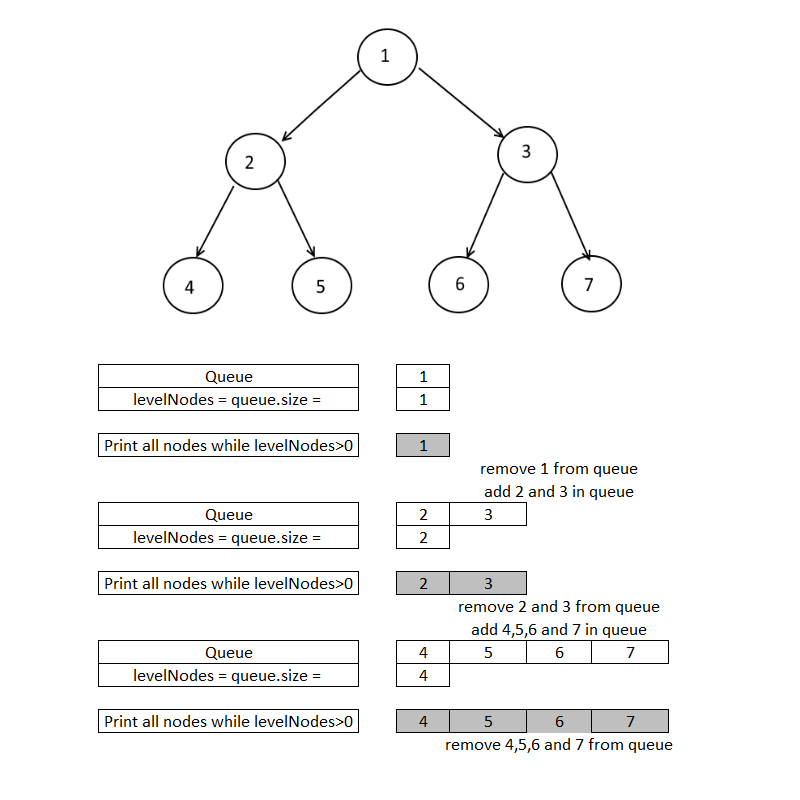
- Do the level order traversal using the queue(Breadth First Search). Click here to learn about how to level order traversal.
- For getting all the nodes at each level, before you take out a node from the queue, store the size of the queue in a variable, say you call it levelNodes.
- Now while levelNodes>0, take out the nodes print it, and add their children into the queue.
- After this while loop put a line break.
while(!q.isEmpty()){
levelNodes = q.size();
while(levelNodes>0){
Node n = (Node)q.remove();
System.out.print(" " + n.data);
if(n.left!=null) q.add(n.left);
if(n.right!=null) q.add(n.right);
levelNodes--;
}
System.out.println("");
}
- Since we had taken the queue size before we added new nodes, we will get the count at each level and after printing this count, put a line break, see the example below
Output by Naive Approach : 5 10 15 20 25 30 35 Output by Better Approach : 5 10 15 20 25 30 35