|
This post is completed by 1 user
|
Add to List |
143. Merge K Sorted Arrays
Objective: Given a k-sorted array, write an algorithm to merge these into one sorted array.
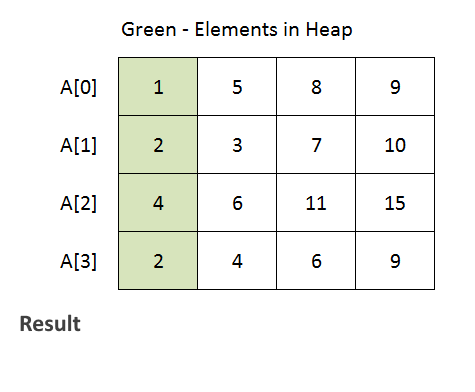
Example :
[
[1, 3, 5],
[2, 4, 6],
[0, 7, 8, 9]
]
Output: Merged Array: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Naive Solution: O(nkLognk)
- Create a result[] of size n*k.
- Copy all the elements from k arrays into the result array. This will take O(nk).
- Sort the result[] using Merge Sort. This will take O(nkLognk) time.
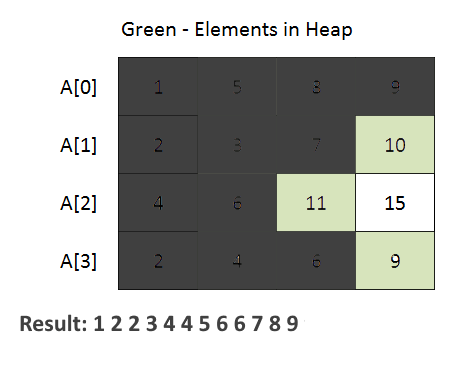
Better Approach: O(nkLogk)
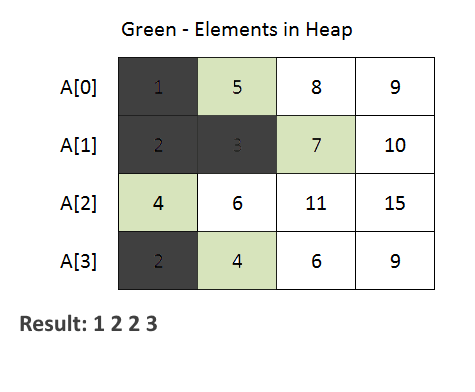
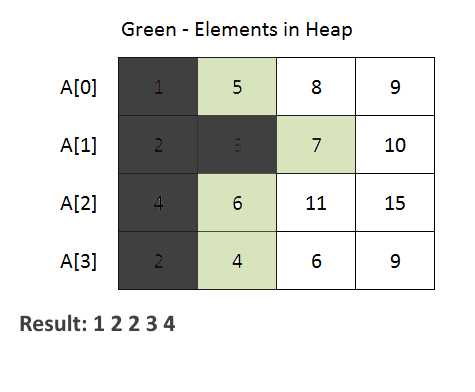
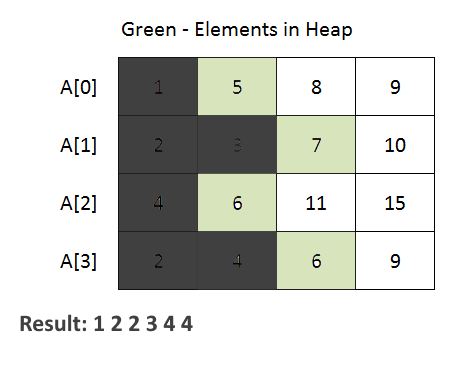
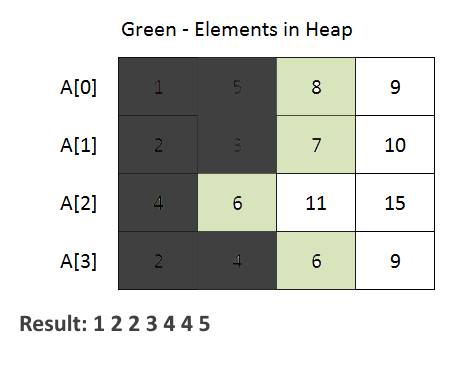
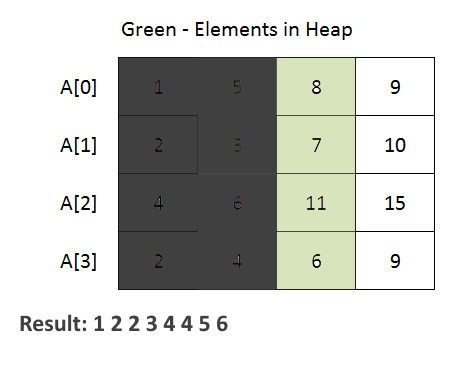
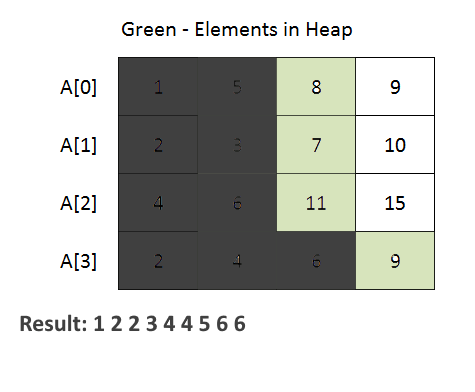
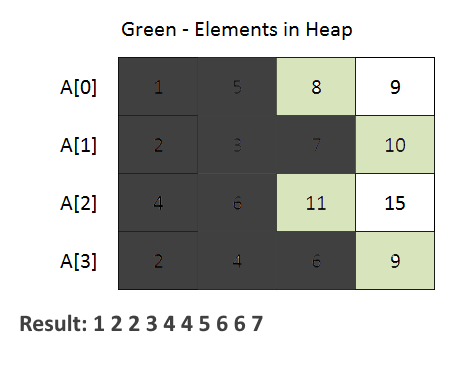
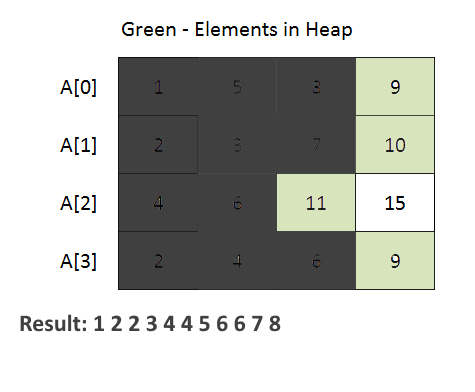
- The code begins with the definition of a Node class. This class is used to represent an element from one of the input arrays. It contains attributes for the element value, array index (element belongs to which of the given k arrays), and element index within the array.
- PriorityQueue (min-heap) to efficiently merge the arrays. The priority queue is initialized with a comparator that compares Node objects based on their element values. This ensures that the minimum element is always at the top of the priority queue.
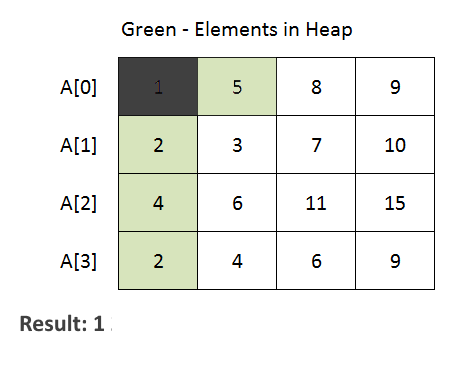
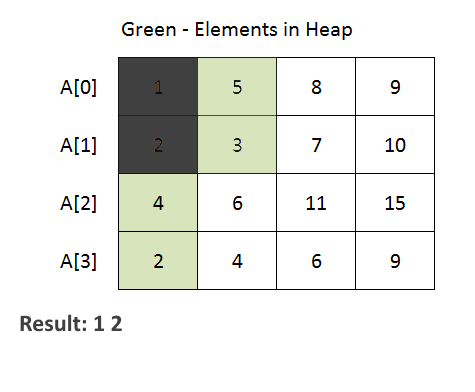
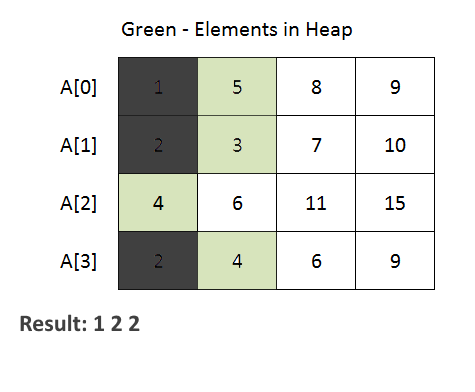
- The method iterates through each array and adds the first element of each array to the priority queue. Then, it repeatedly extracts the minimum element from the priority queue and adds it to the merged list. If there are more elements in the same array (use array index to achieve this), they are added to the priority queue for further processing.
- See the animation below for a better understanding.
[1, 2, 2, 3, 4, 4, 5, 6, 6, 7, 8, 9, 9, 9, 10, 11, 14, 15, 16, 19]