|
Be the first user to complete this post
|
Add to List |
281. Prim’s Algorithm - Minimum Spanning Tree (MST)
What is Prim’s algorithm?
- Prim's algorithm is a greedy algorithm.
- It finds a minimum spanning tree for a weighted undirected graph.
- This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
- The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
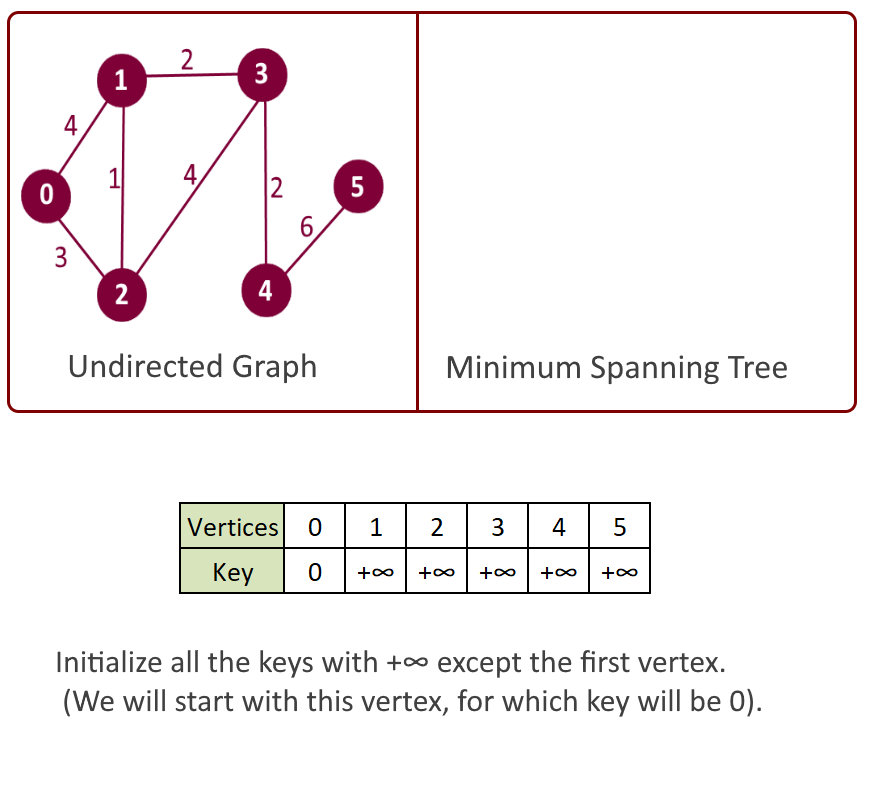
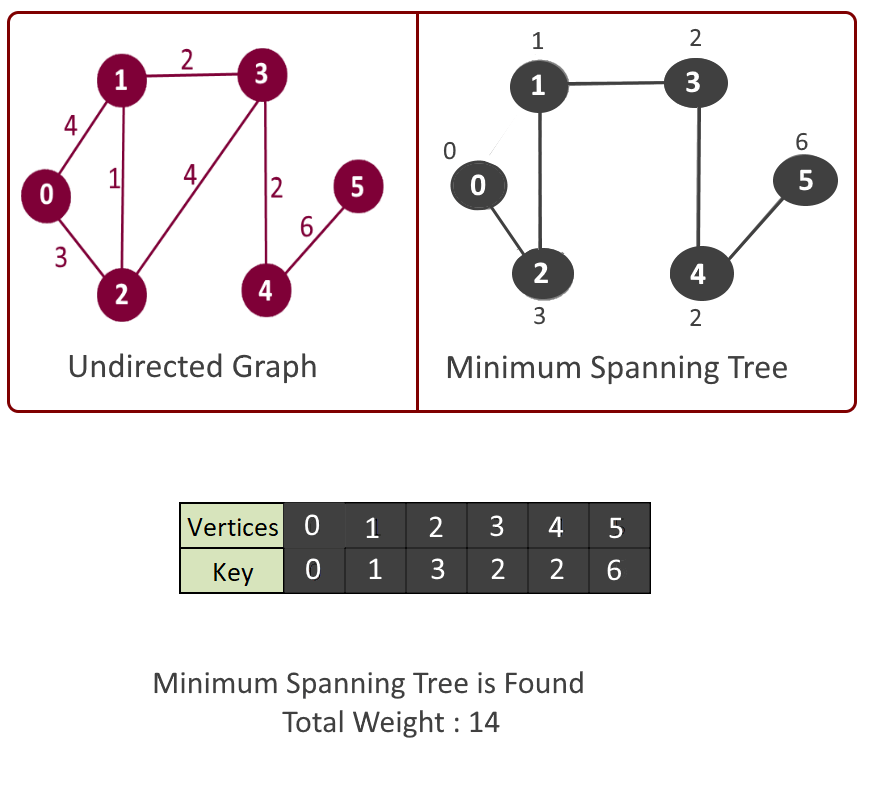
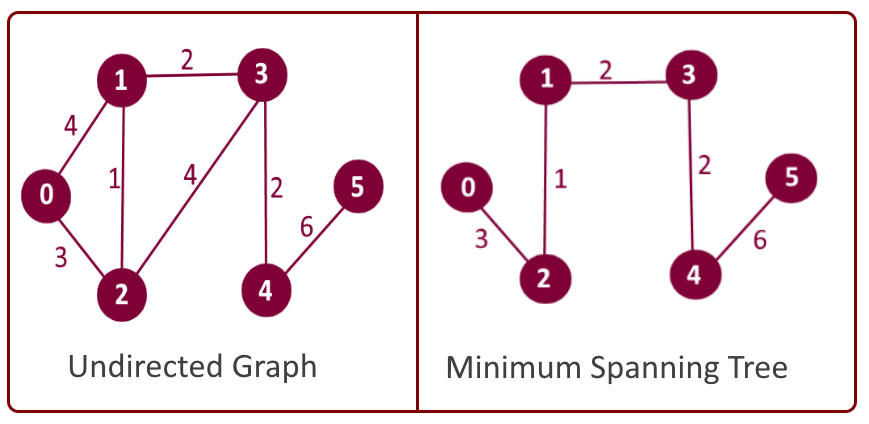
Example:
How to implement Prim’s algorithm?
- Start with the empty spanning tree.
- Maintain a set mst[] to keep track to vertices included in minimum spanning tree.
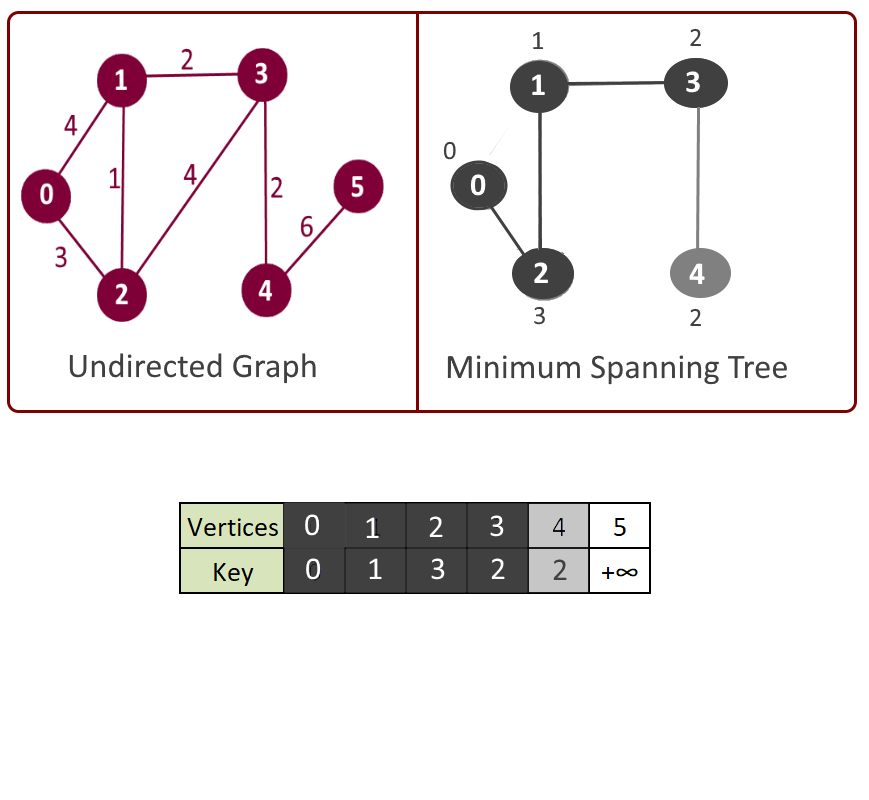
- Assign a key value to all the vertices, (say key []) and initialize all the keys with +∞ (Infinity) except the first vertex. (We will start with this vertex, for which key will be 0).
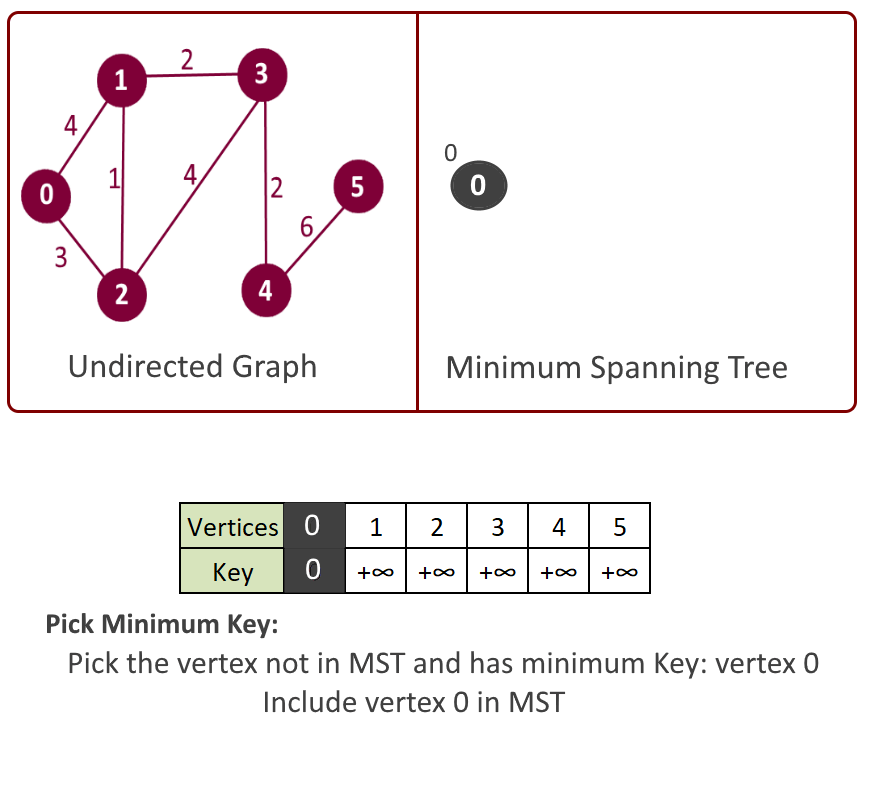
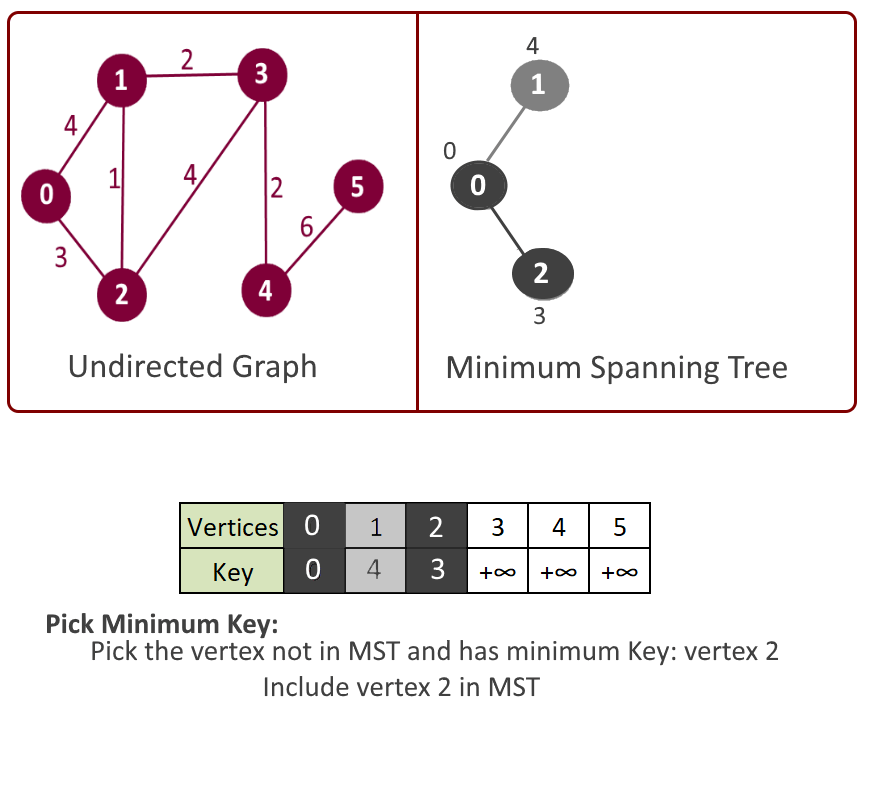
- Key value in step 3 will be used in making decision that which next vertex and edge will be included in the mst[]. We will pick the vertex which is not included in mst[] and has the minimum key. So at the beginning the first vertex will be picked first.
- Repeat the following steps until all vertices are processed
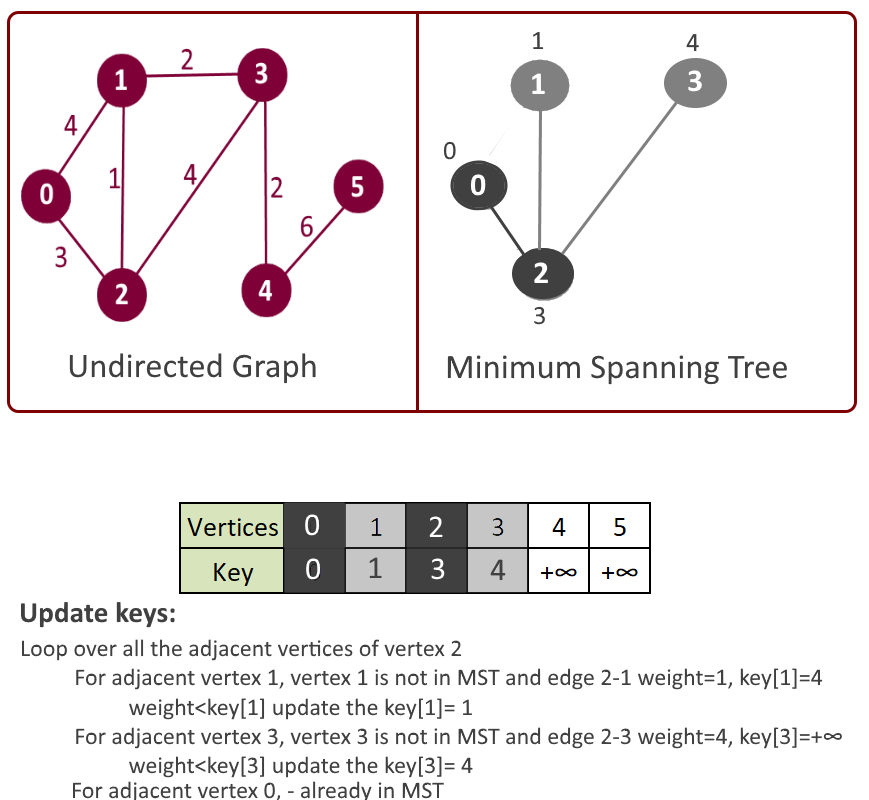
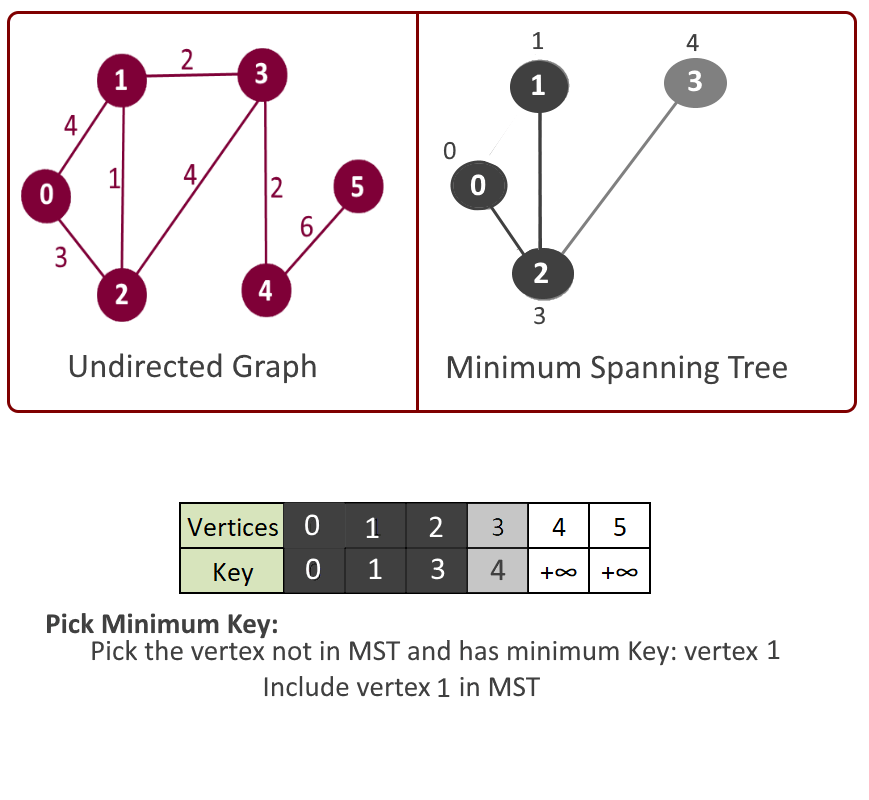
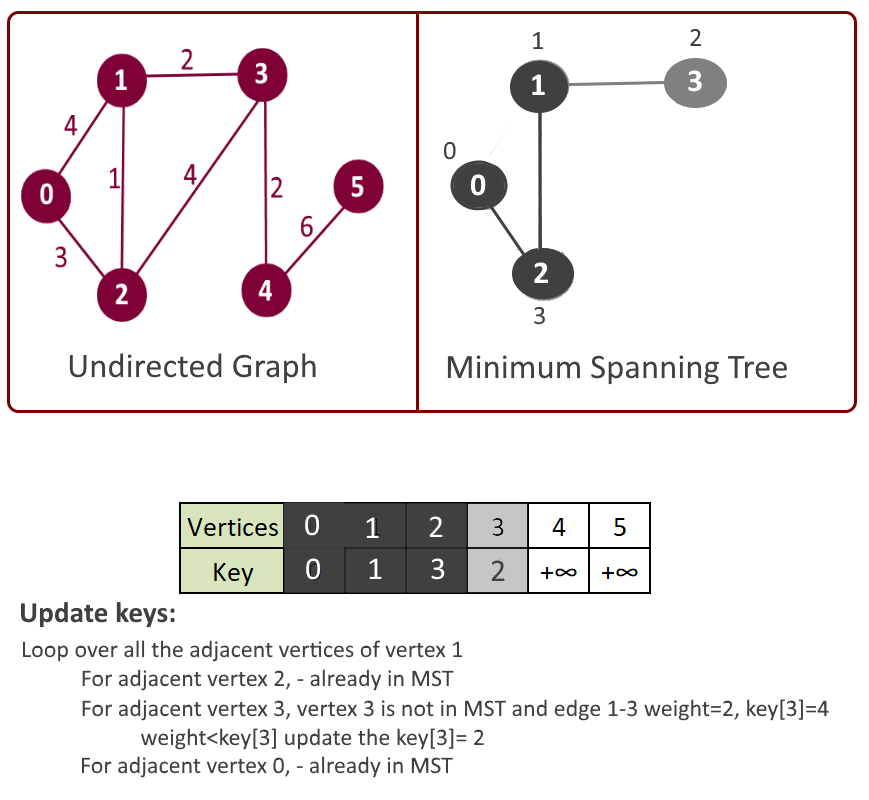
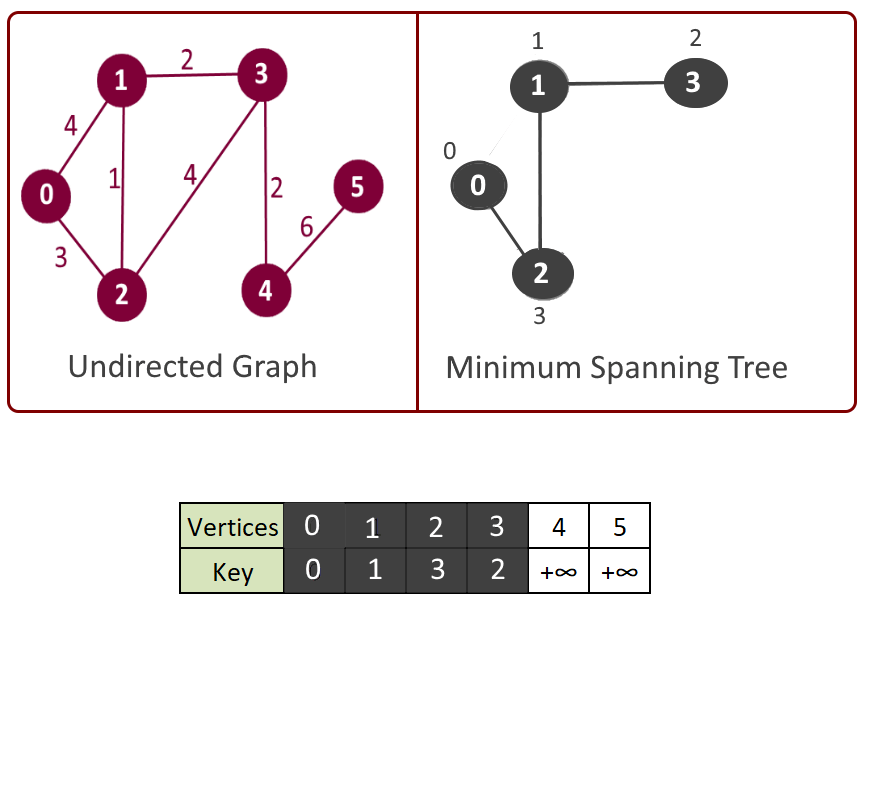
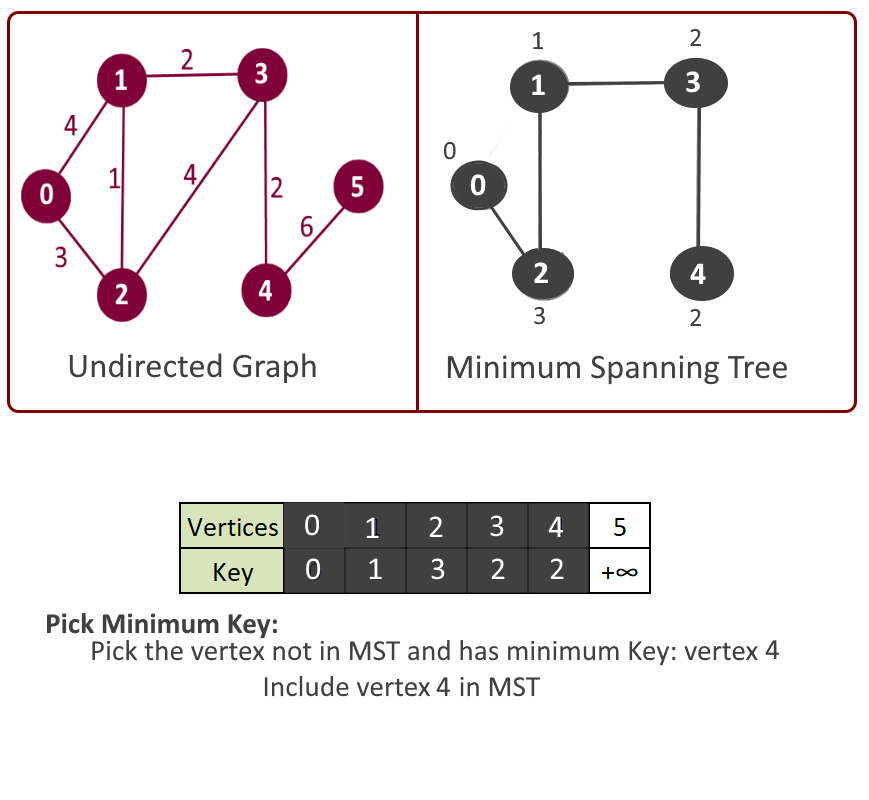
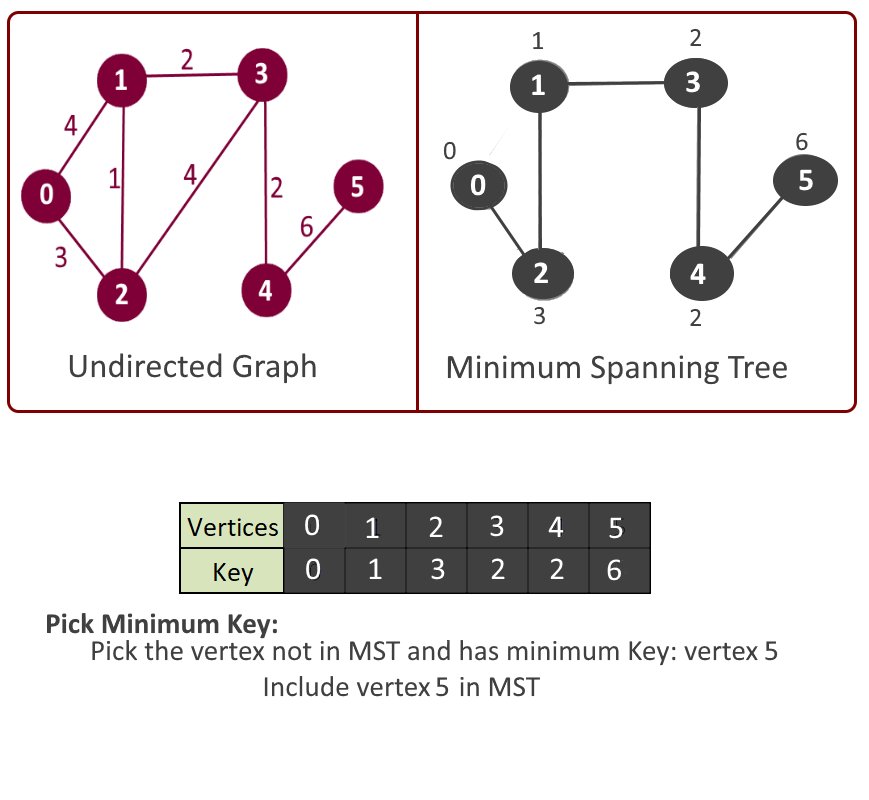
- Pick the vertex u which is not in mst[] and has minimum key.
- Add vertex u to mst[].
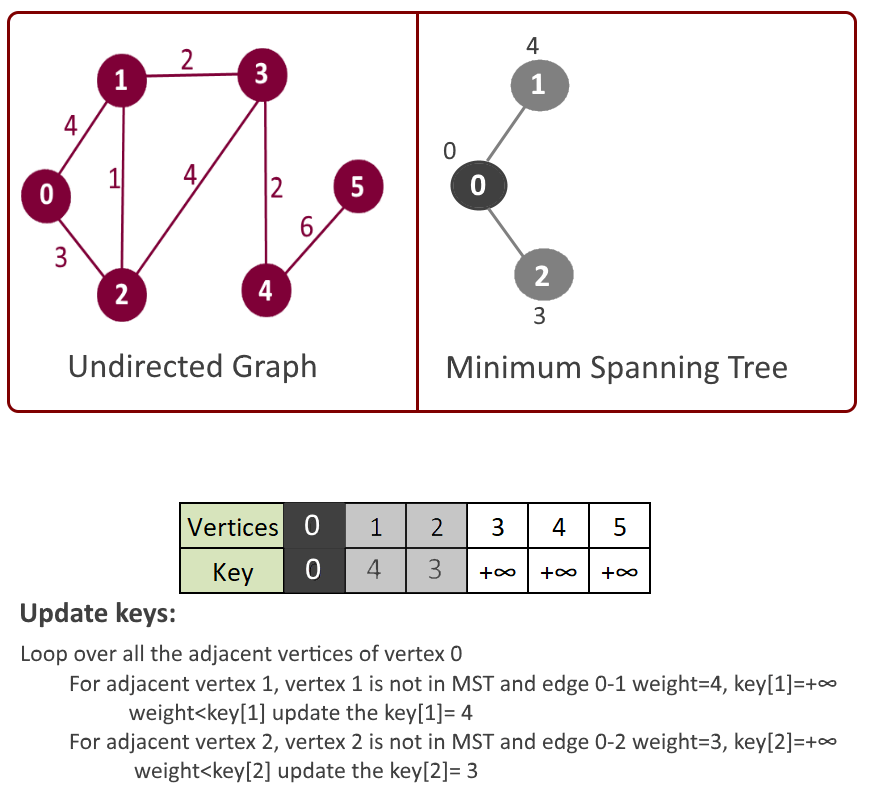
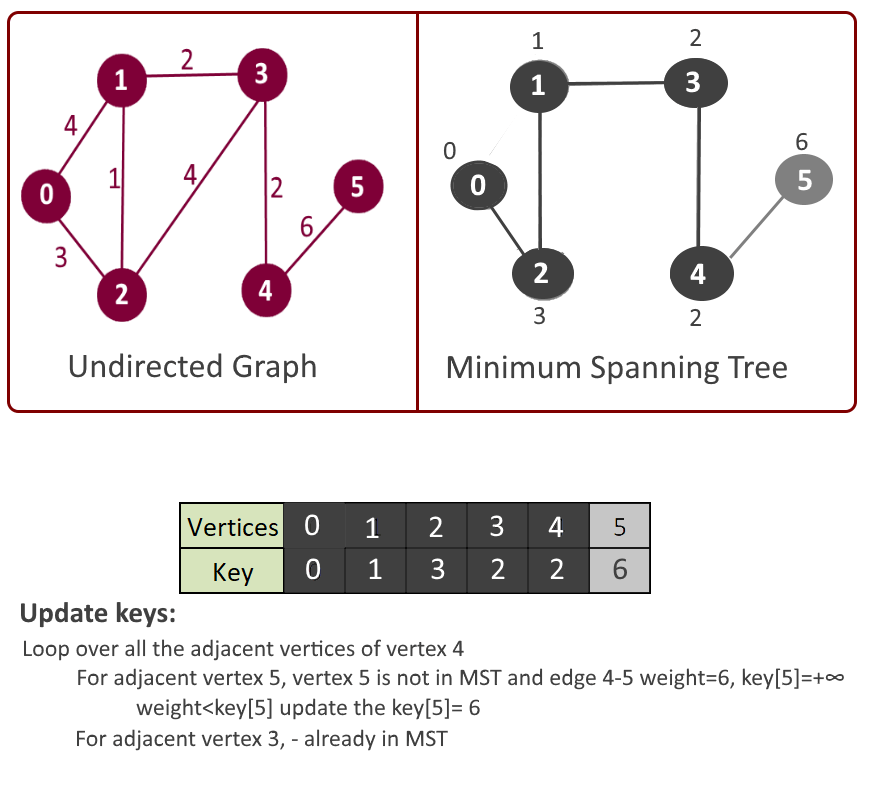
- Loop over all the adjacent vertices of u
- For adjacent vertex v, if v is not in mst[] and edge u-v weight is less than the key of vertex u, key[u] then update the key[u]= edge u-v weight.
- Return mst[].
Please see the animation below for better understanding.
Ways to Implement:
- Adjacency Matrix – Searching.
- Adjacency List – Binary Heap
- Adjacency List – Priority Queue with decrease key.
- Adjacency List - Priority Queue without decrease key – Better
Time Complexity:
The time complexity of Prim's algorithm depends on the data structures used for the graph and for ordering the edges by weight.
| Data Structure of Graph | Ordering | Time Complexity |
| Adjacency Matrix | Searching | O(|V|2) |
| Adjacency List | Binary Heap | O(|E|log|V|) |
| Adjacency List | Priority Queue with decrease key | O(|E|2log|V|) |
| Adjacency List | Priority Queue without decrease key – Better Implementation | O(|E|log|V|) |
Reference - Wiki