|
Be the first user to complete this post
|
Add to List |
283. Prim’s – Minimum Spanning Tree (MST) |using Adjacency List and Min Heap
Earlier we have seen what is Prim’s algorithm is and how it works. In this article we will see its implementation using adjacency list and Min Heap.
We strongly recommend to read - prim’s algorithm and how it works and implementation of min-Heap
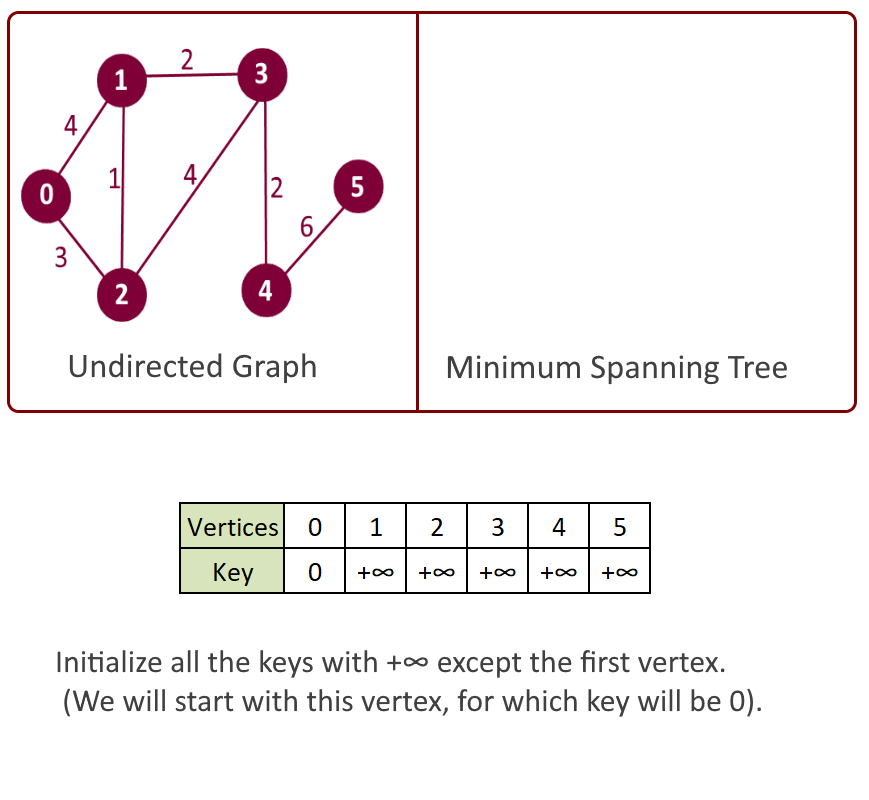
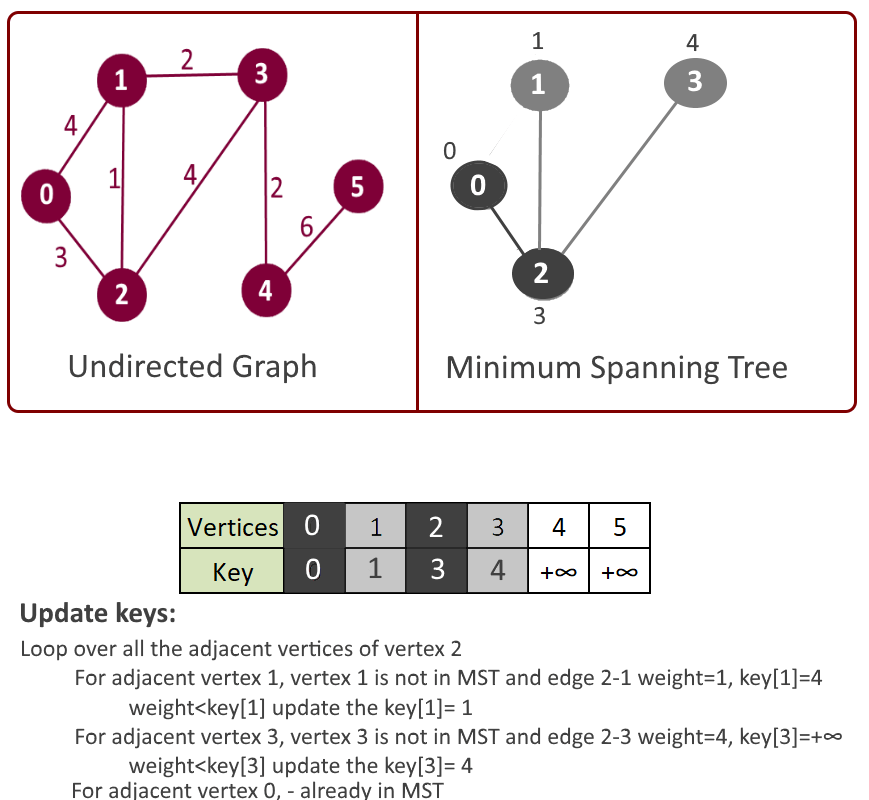
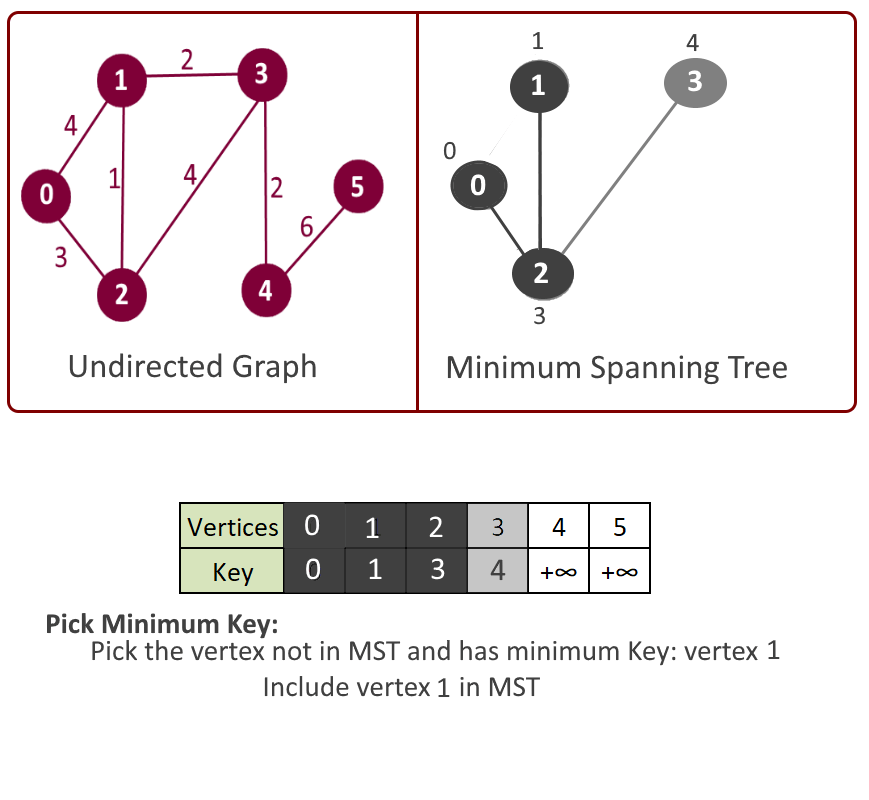
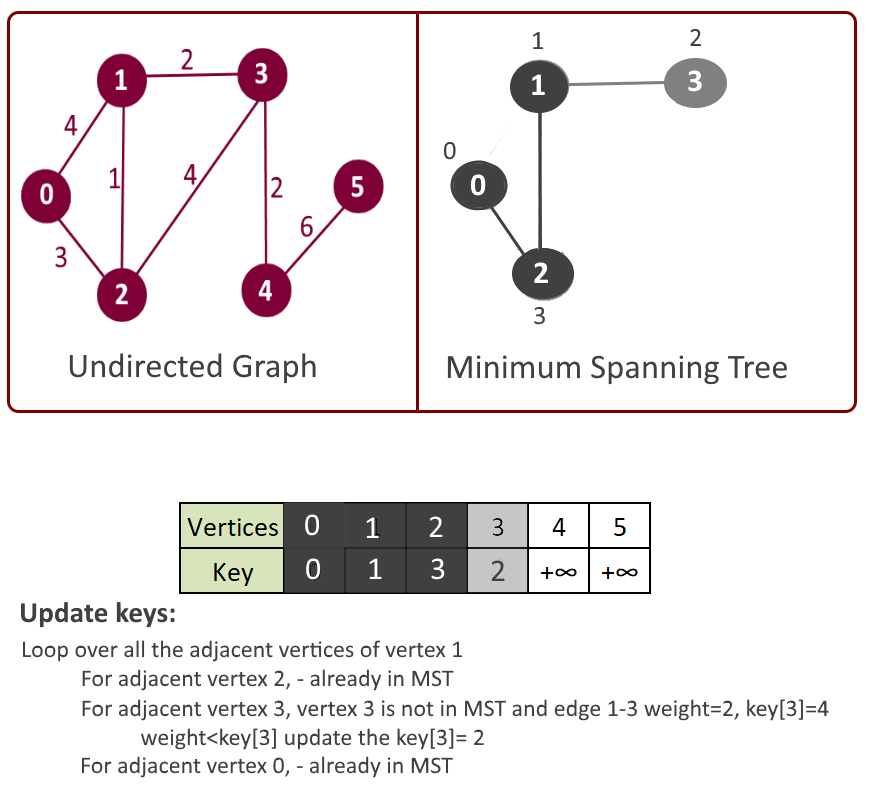
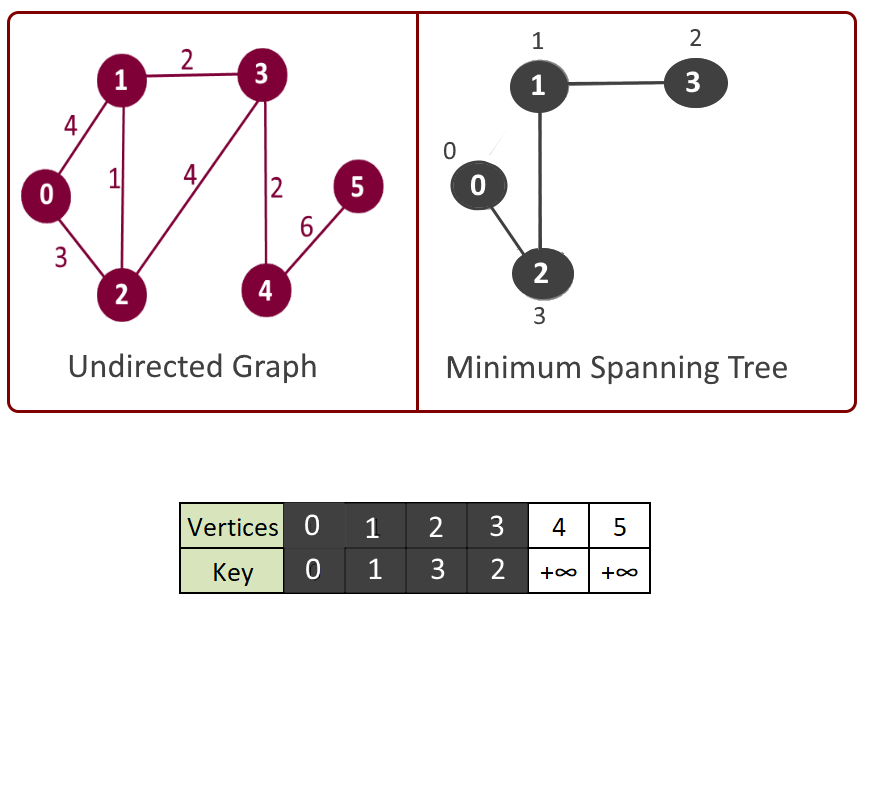
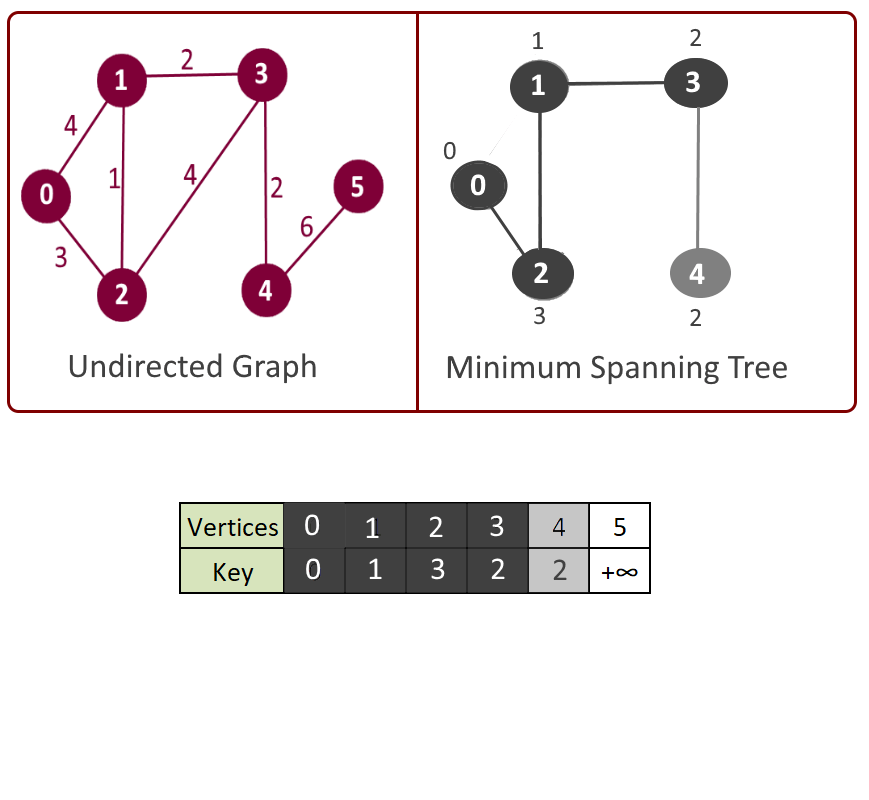
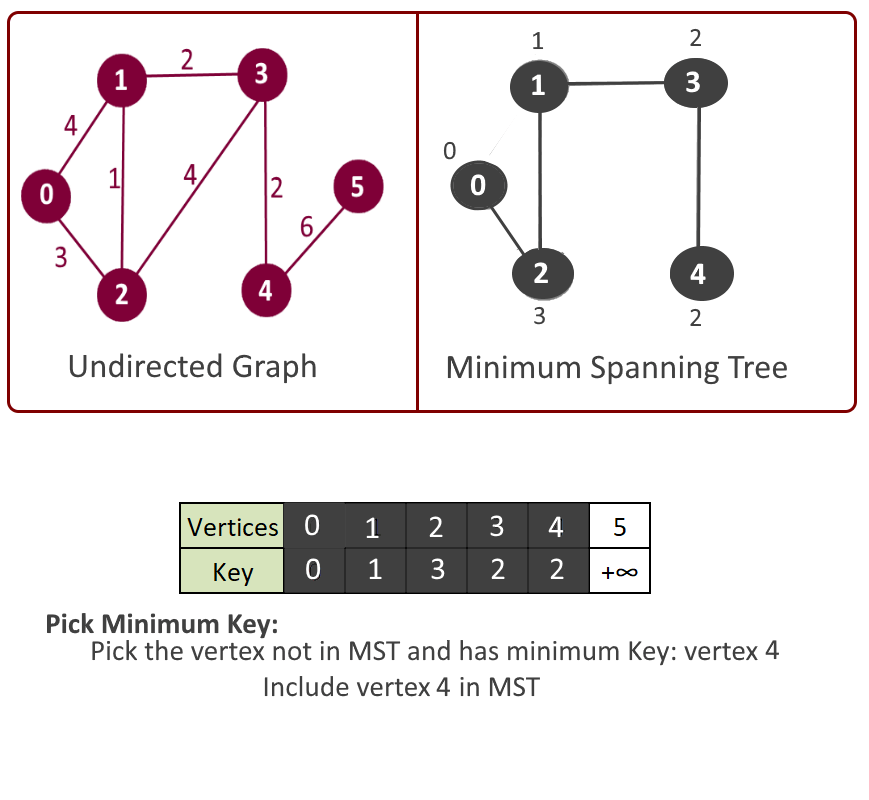
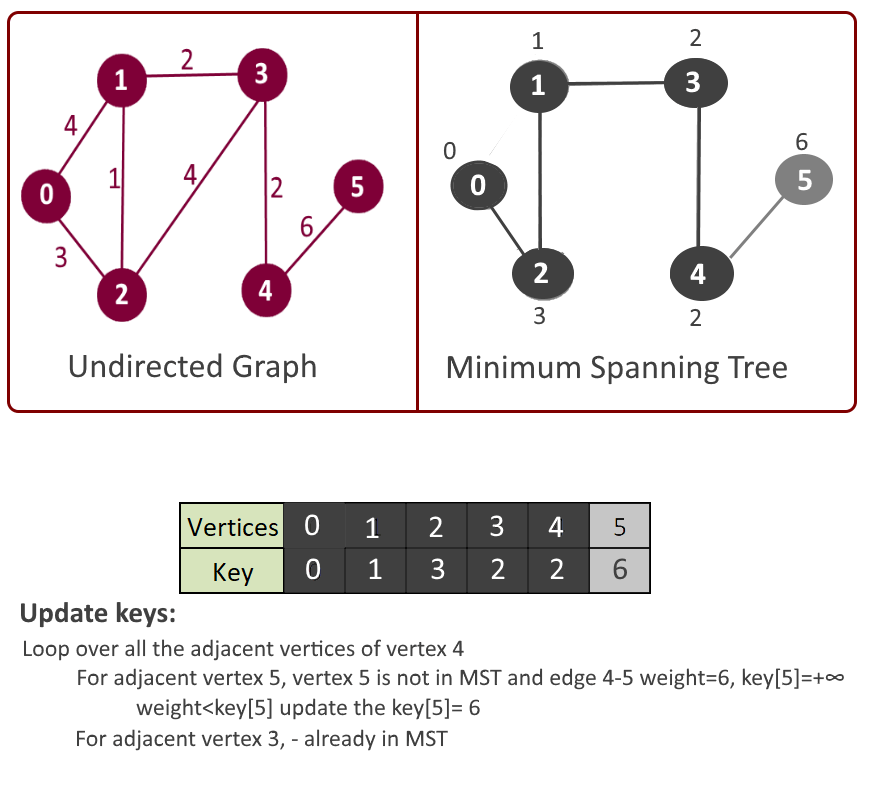
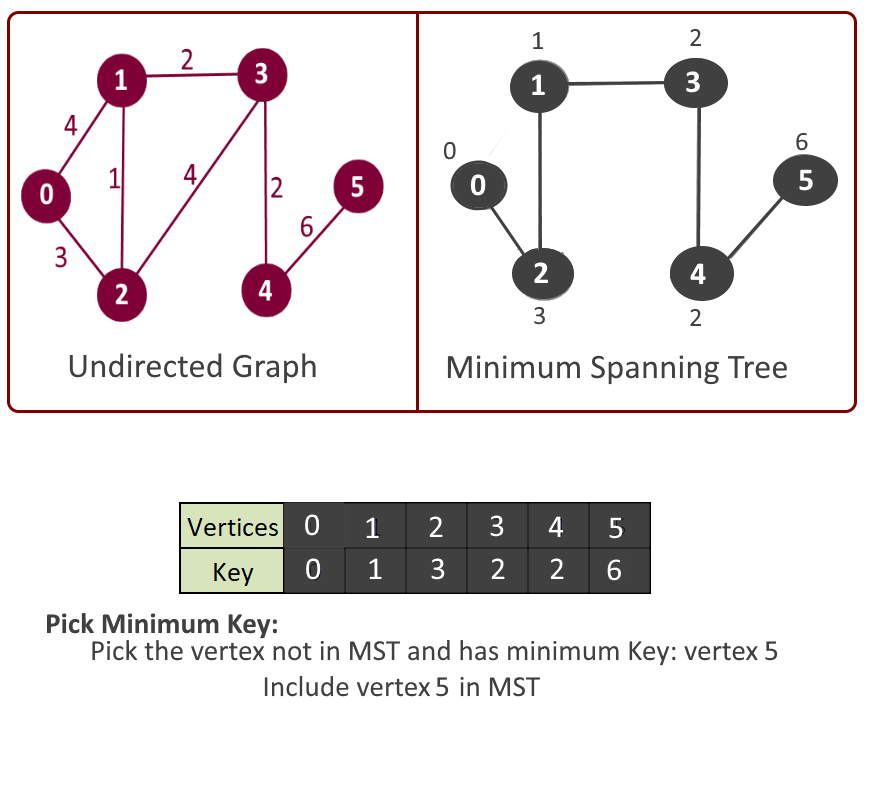
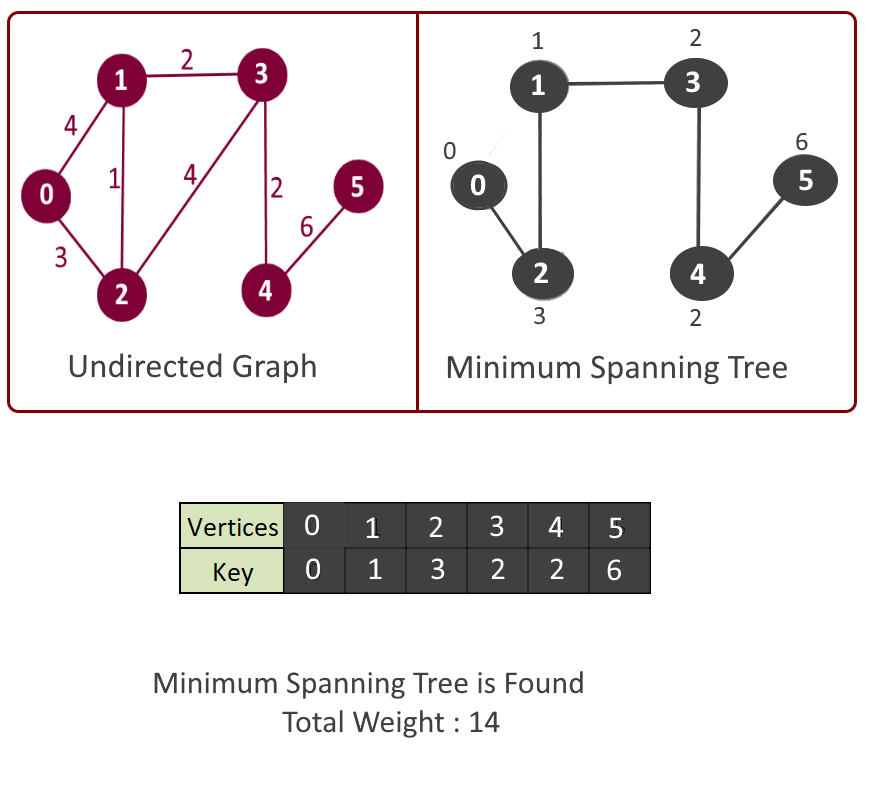
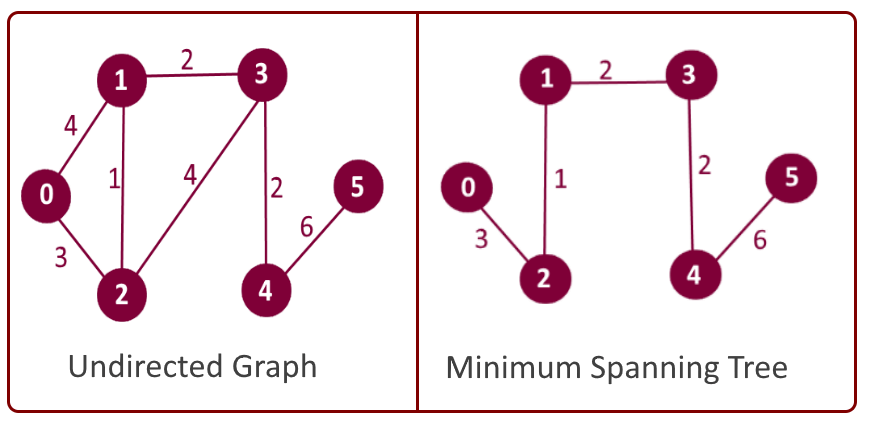
Example:
Implementation – Adjacency List and Min Heap
- Create min Heap of size = no of vertices.
- Create a heapNode for each vertex which will store two information. a). vertex b). key
- Use inHeap[] to keep track of the vertices which are currently in min heap.
- Create key[] to keep track of key value for each vertex. (keep updating it as heapNode key for each vertex)
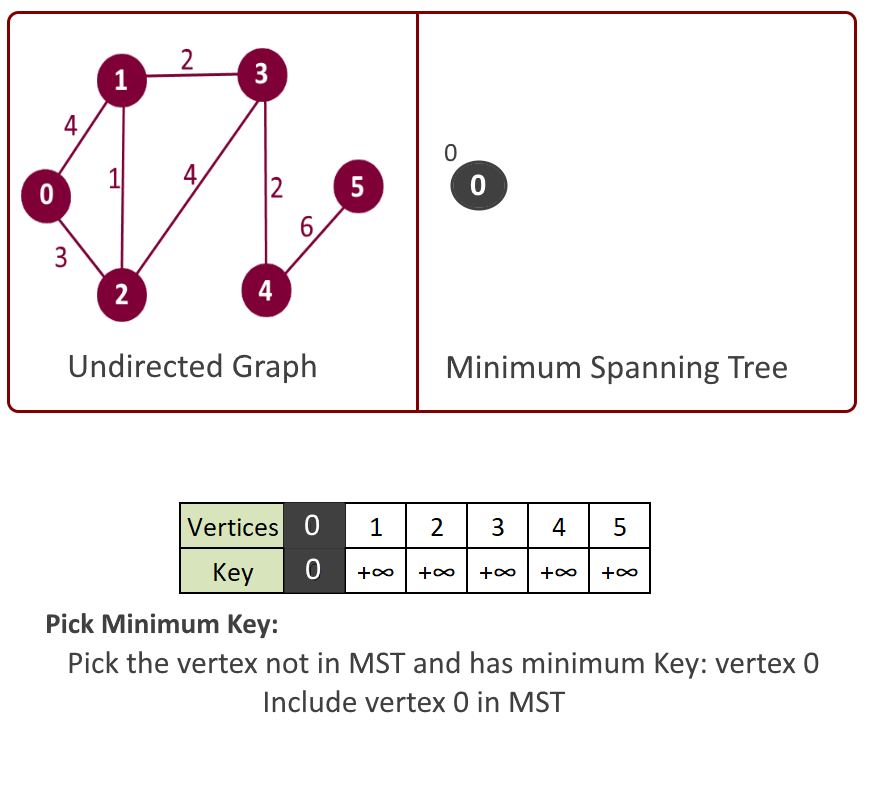
- For each heapNode, Initialize key as MAX_VAL except the heapNode for the first vertex for which key will 0. (Start from first vertex).
- Insert all the heapNodes into min heap. inHeap[v] = true for all vertices.
- while minHeap is not empty
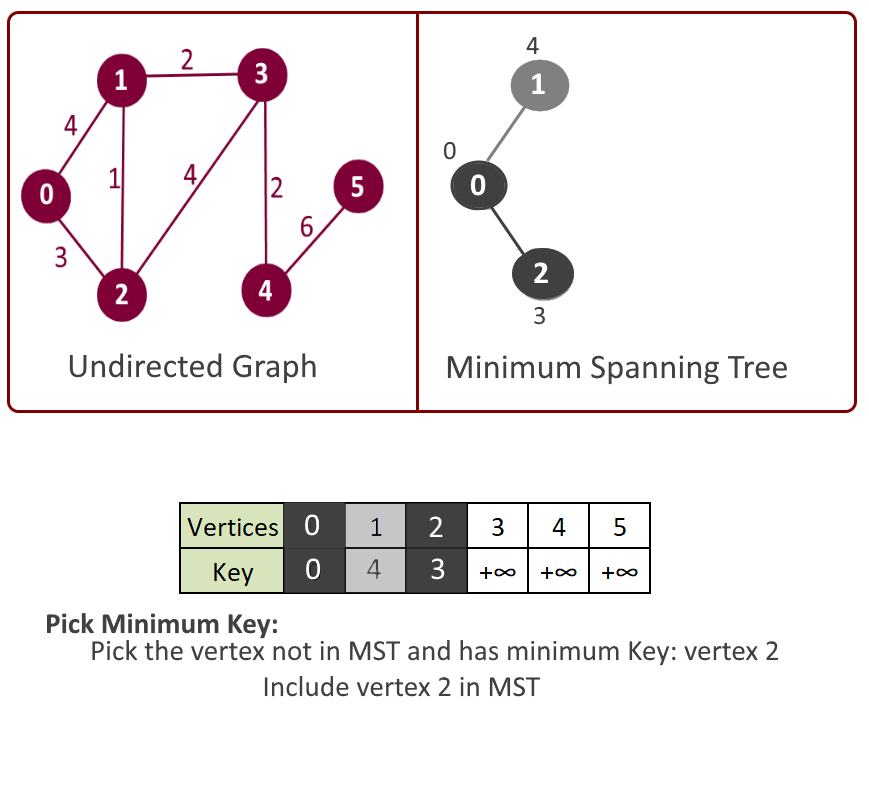
- Extract the min node from the heap, say it vertex u and add it to the MST.
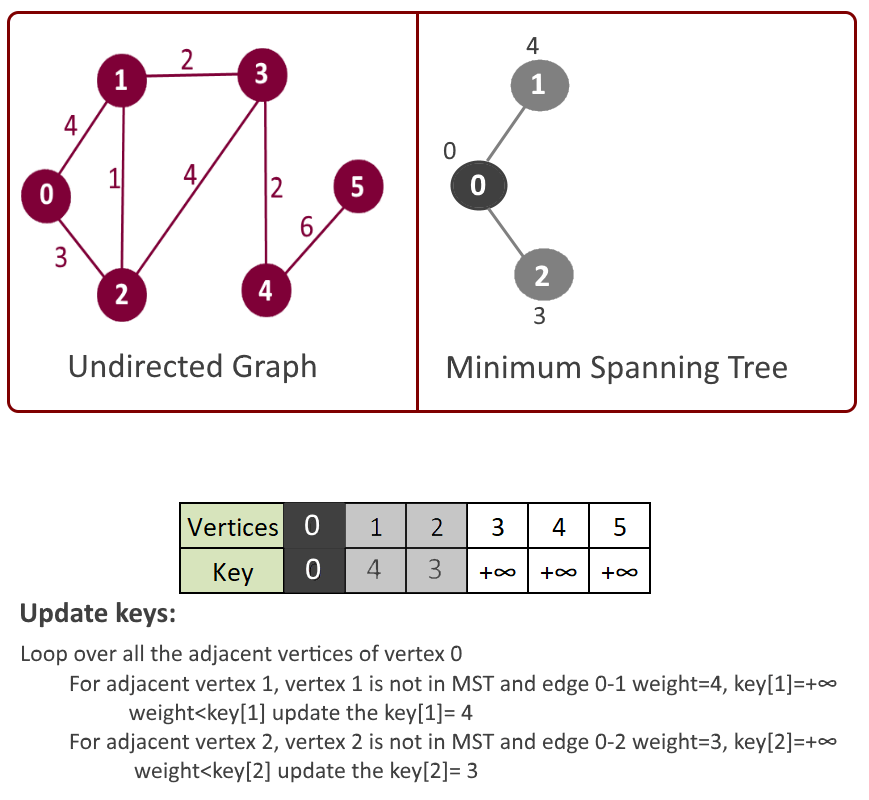
- Decrease key: Iterate through all the adjacent vertices of above vertex u and if adjacent vertex (say it’s v) is still part of inHeap[] (means not in MST) and key of vertex v> u-v weight then key of vertex v = u-v
- We will use Result object to store the result of each vertex. Result object will store 2 information’s.
- First the parent vertex, means from which vertex you can visit this vertex. Example if for vertex v, you have included edge u-v in mst[] then vertex u will be the parent vertex.
- Second weight of edge u-v. If you add all these weights for all the vertices in mst[] then you will get Minimum spanning tree weight.
Time Complexity:
Total vertices: V, Total Edges : E
- O(logV) – to extract each vertex from queue. So for V vertices – O(VlogV)
- O(logV) – each time decrease the key value of a vertex. Decrease key will be called for at most once for each edge. So for total E edge – O(ElogV)
- So over all complexity: O(VlogV) + O(ElogV) = O((E+V)logV) = O(ElogV)
See the animation below for more understanding
Minimum Spanning Tree: Edge: 1 - 2 weight: 1 Edge: 2 - 0 weight: 3 Edge: 3 - 1 weight: 2 Edge: 4 - 3 weight: 2 Edge: 5 - 4 weight: 6 Total minimum key: 14