|
Be the first user to complete this post
|
Add to List |
282. Prim’s - Minimum Spanning Tree (MST) |using Adjacency Matrix
Earlier we have seen what is Prim’s algorithm is and how it works. In this article we will see its implementation using adjacency matrix.
We strongly recommend to read - prim’s algorithm and how it works.
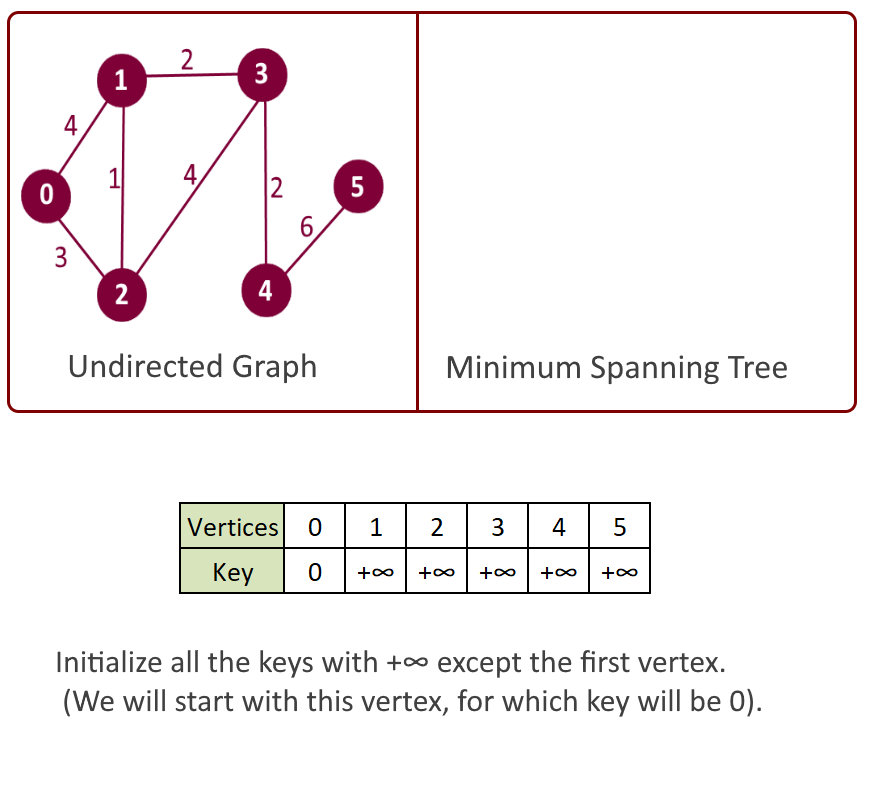
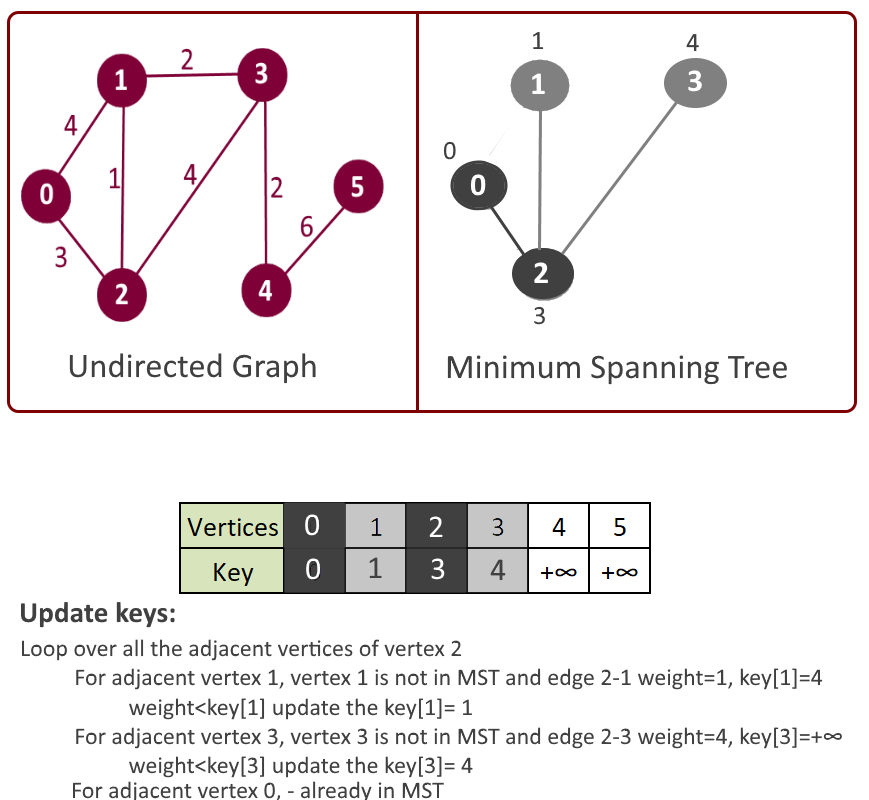
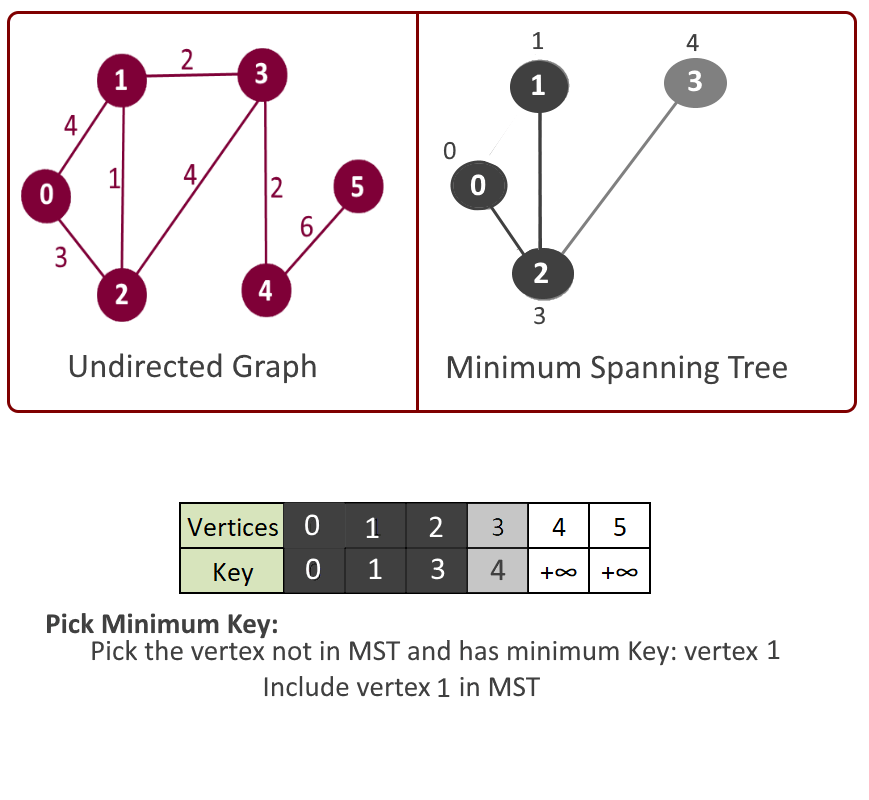
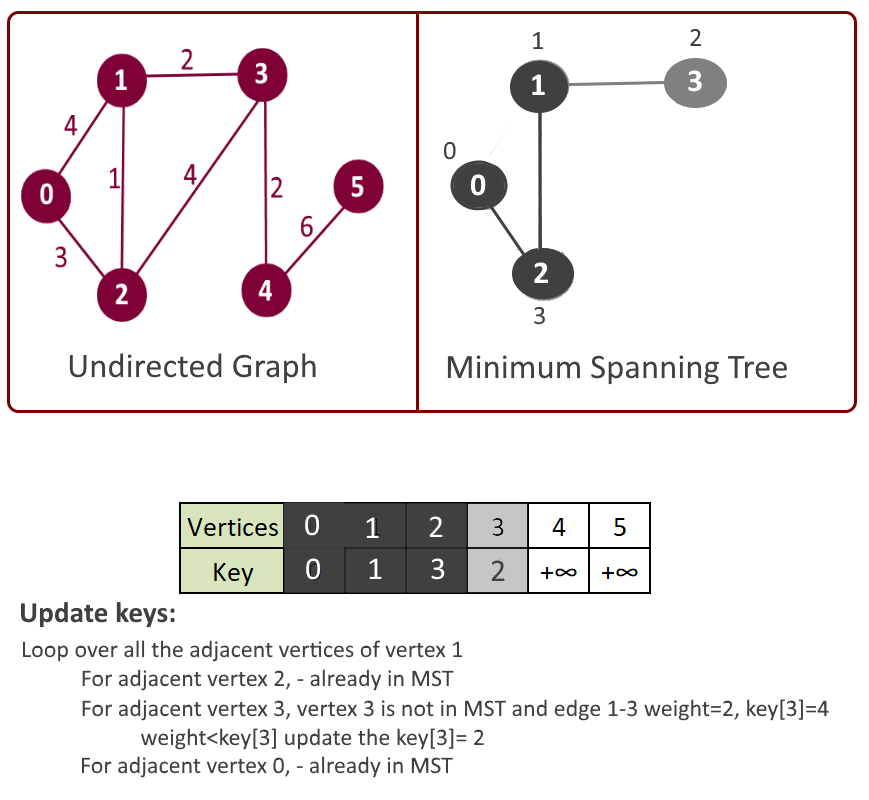
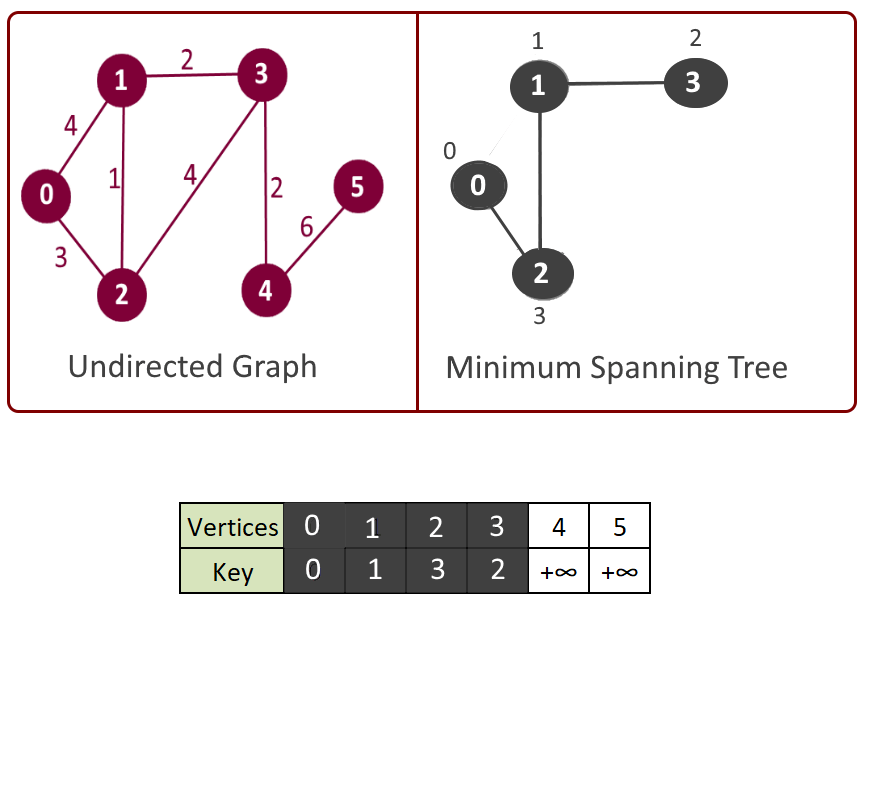
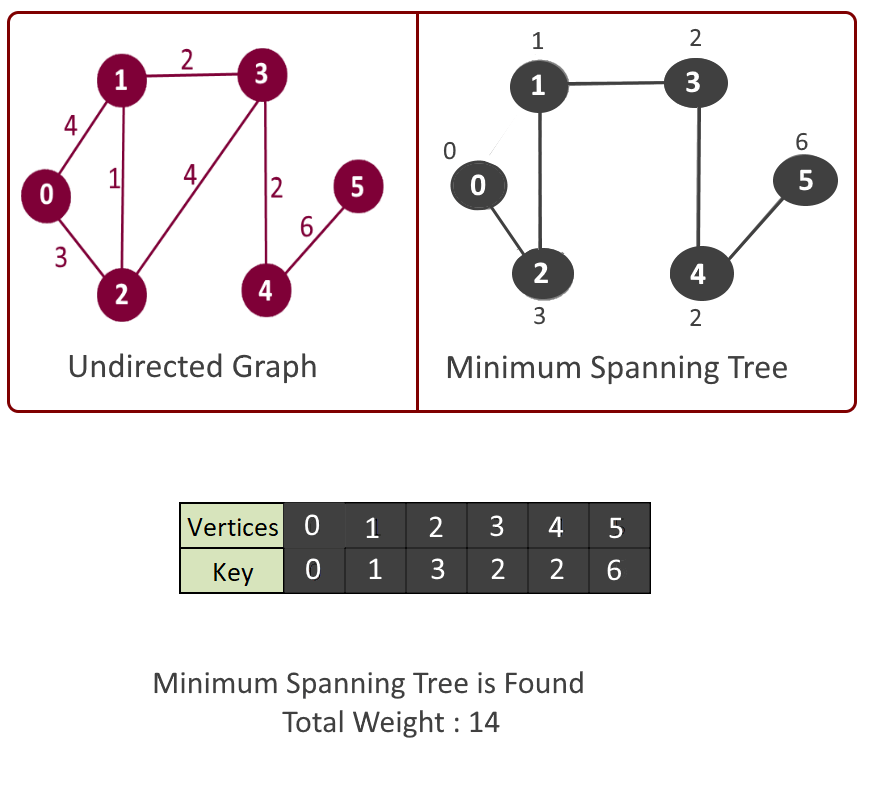
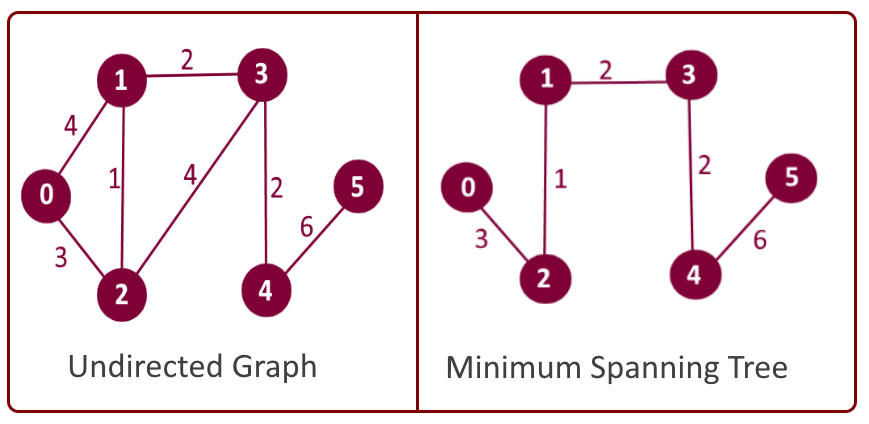
Example:
Implementation – Adjacency Matrix
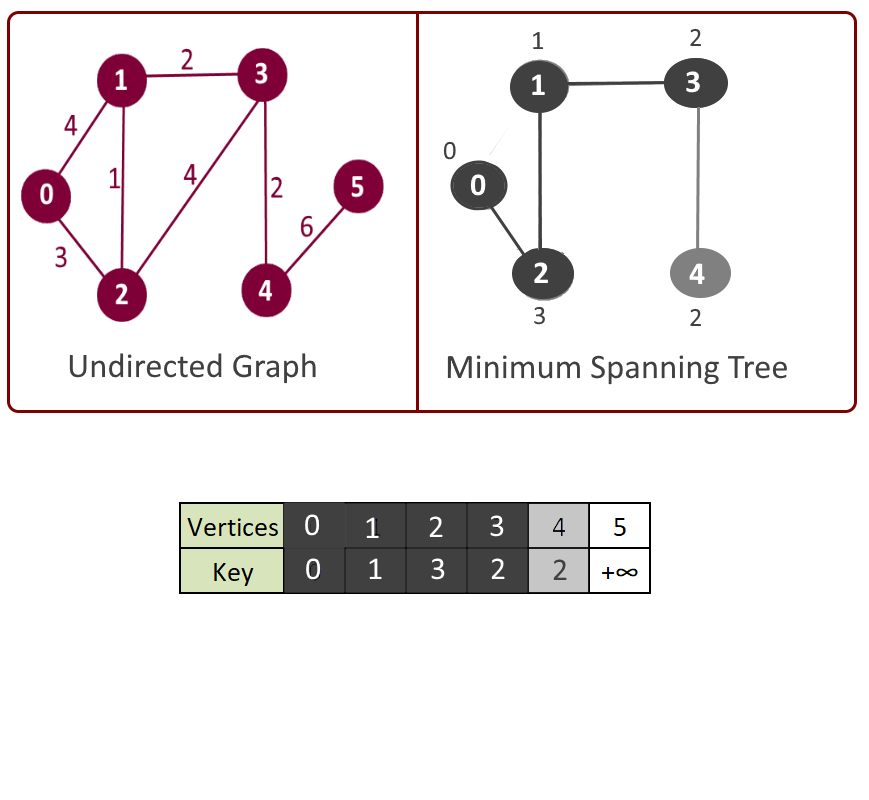
- Create mst[] to keep track of vertices included in MST.
- Create key[] to keep track of key value for each vertex. Which vertex will be included next into MST will be decided based on the key value.
- Initialize key for all vertices as MAX_VAL except the first vertex for which key will 0. (Start from first vertex).
- While(all the vertices are not in MST).
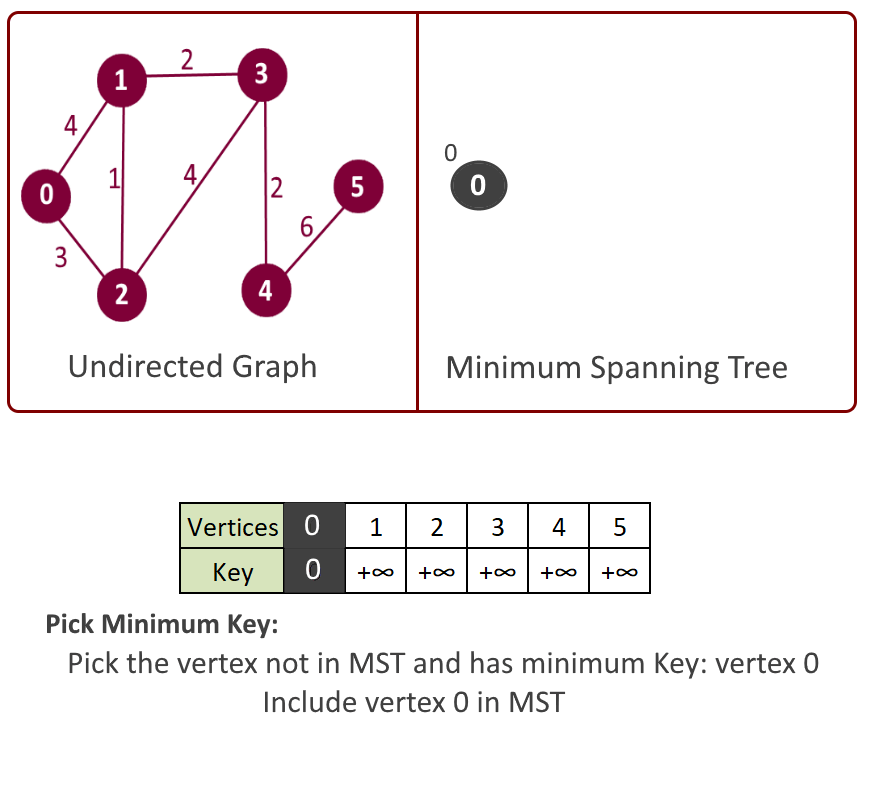
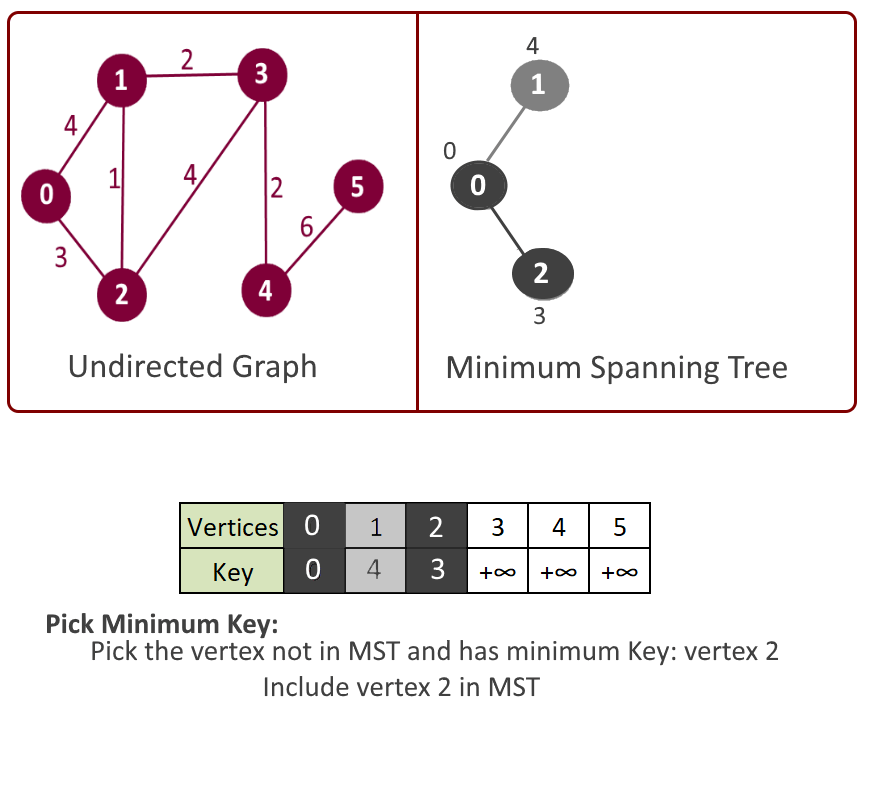
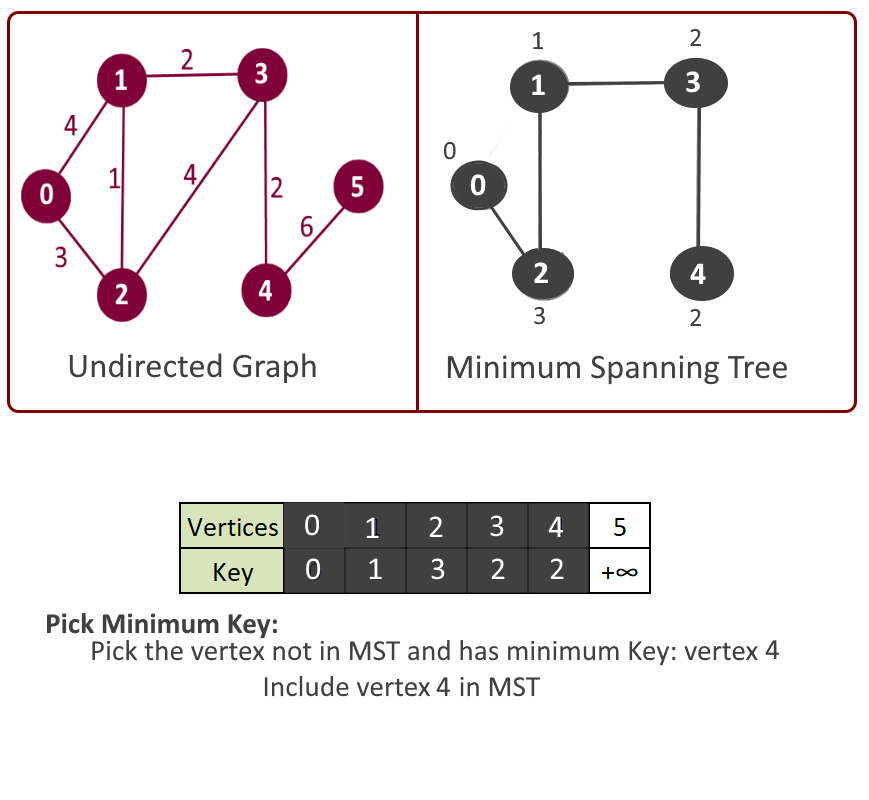
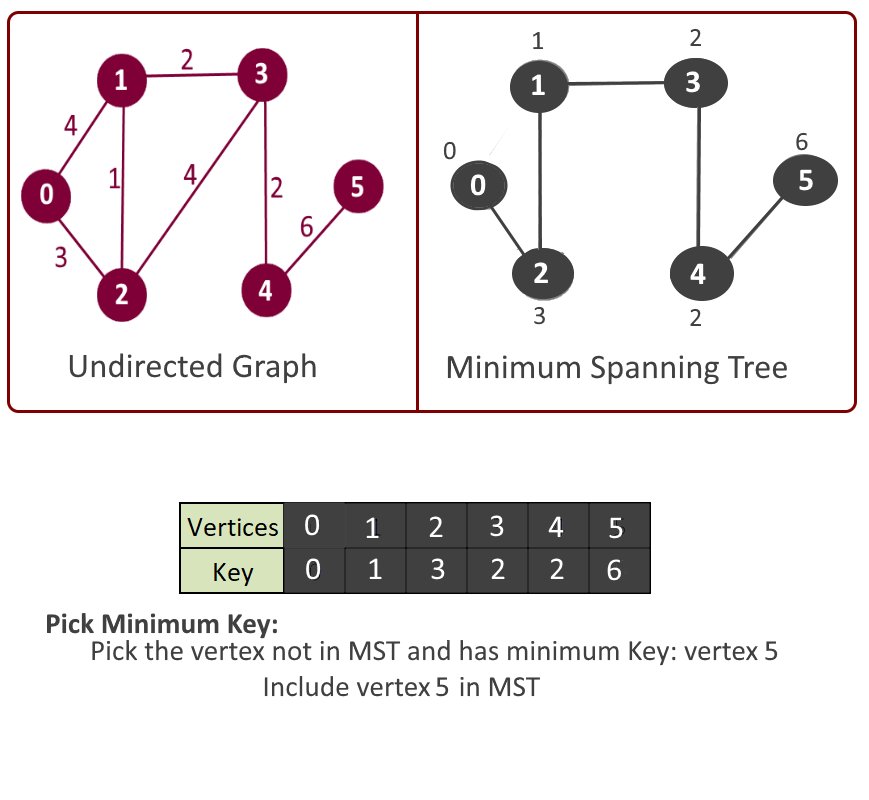
- Get the vertex with the minimum key. Say its vertex u.
- Include this vertex in MST and mark in mst[u] = true.
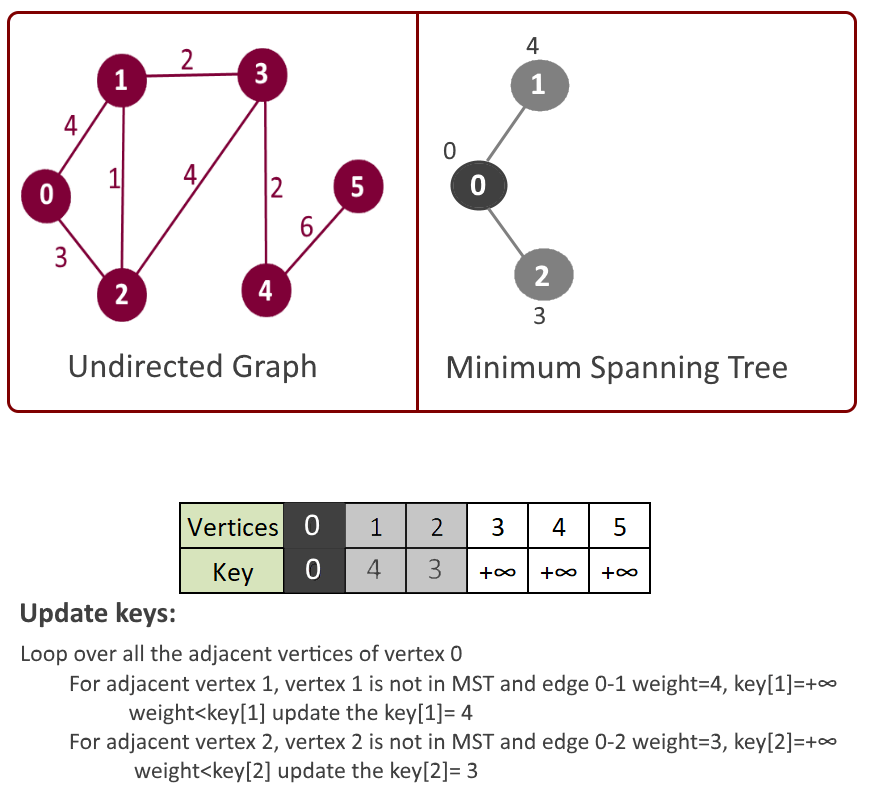
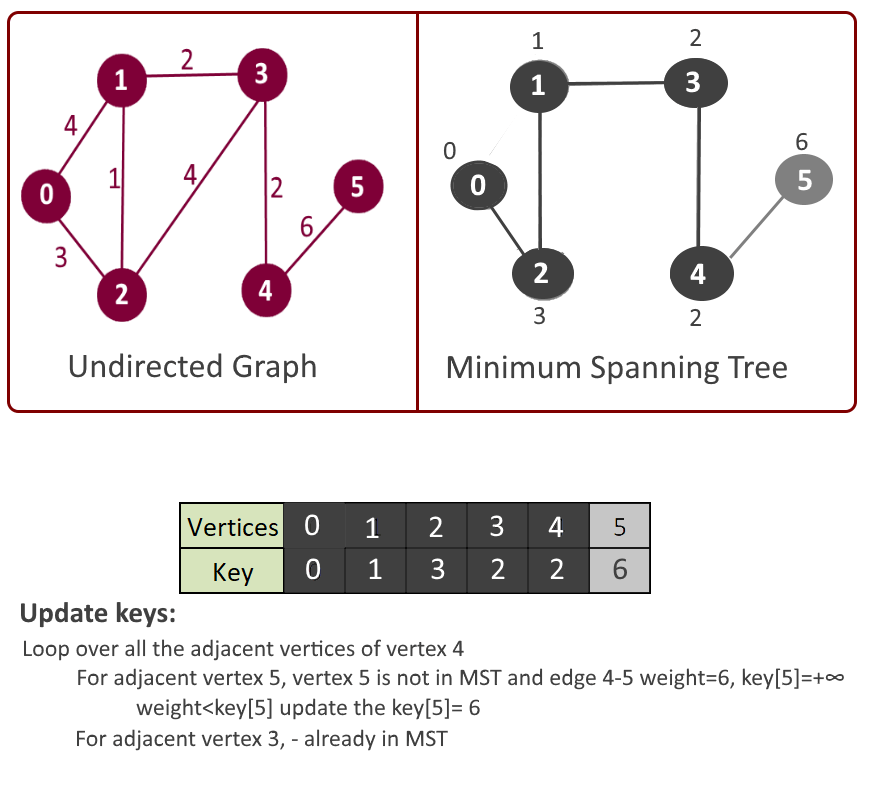
- Iterate through all the adjacent vertices of above vertex u and update the keys if adjacent vertex is not already part of mst[].
- We will use Result object to store the result of each vertex. Result object will store 2 information’s.
- First the parent vertex, means from which vertex you can visit this vertex. Example if for vertex v, you have included edge u-v in mst[] then vertex u will be the parent vertex.
- Second weight of edge u-v. If you add all these weights for all the vertices in mst[] then you will get Minimum spanning tree weight.
- See the code for more understanding. Go through the commented description.
Time Complexity: O(|V|2).
Please see the animation below for better understanding.
Output:
Minimum Spanning Tree:
Edge: 1 - 2 key: 1 Edge: 2 - 0 key: 3 Edge: 3 - 1 key: 2 Edge: 4 - 3 key: 2 Edge: 5 - 4 key: 6 Total minimum key: 14