|
This post is completed by 1 user
|
Add to List |
118. Print All Combinations of subset of size K from Given Array
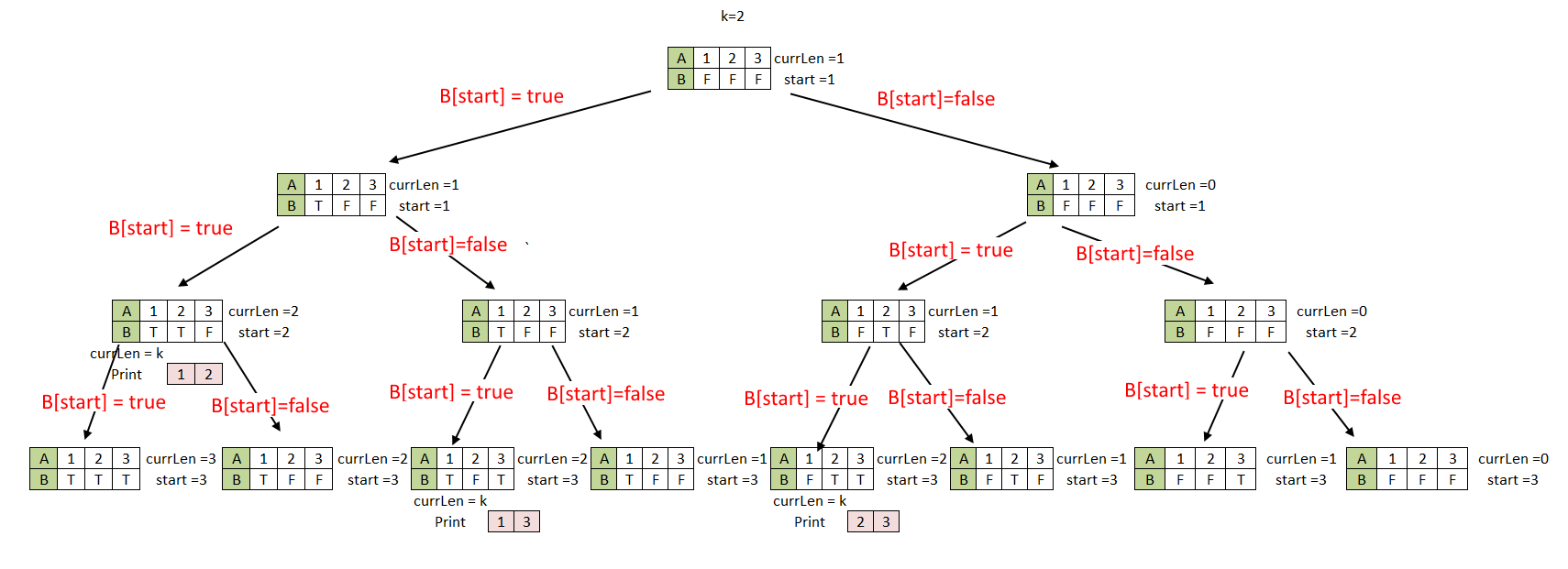
Objective: Given an array of integers of size N, print all the subsets of size k. (k<=N)
Example:
Generate all subsets of a fixed size k of a given set [1,2,3...n]. e.g, if n=5 and k=3, the output will look like
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5
Approach:
- Create an boolean array of the same size as the given array.
- Now for every integer we have two options, whether to select it or ignore it.
- Now if we select it, we will put TRUE in the boolean array at the corresponding index or if we ignore it, put FALSE at that index.
- We will start with currentLength =0 and do the recursive calls for both the options mentioned in the previous step.
- If we select an integer to print, make currentLength +1 and if we ignore, dont change currentLength.
- Another important factor is from which index you will start making the subset of size k. Initialize start = 0, and with every recursive call, make start + 1 ( for both the scenarios mentioned in the steps above).
- Print the elements when currentLength = k.
Note: Click on the image to enlarge it.
Output:
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5

