Print All Possible Subsets with Sum equal to a given Number

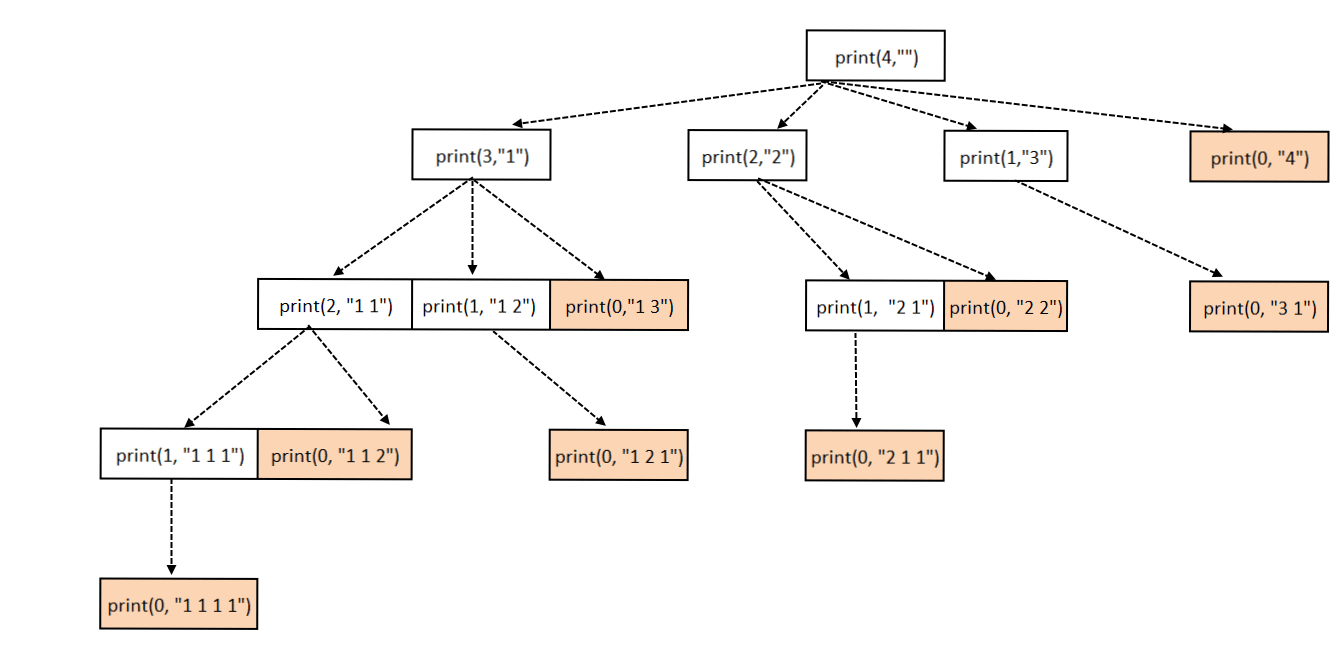
Objective: Given a number N, Write an algorithm to print all possible subsets with Sum equal to N

This question has been asked in the Google for software engineer position.

Example:

N=4

1111
112
121
13
211
22
31
4

 

Approach:

This problem is quite similar to Print All Subsets of a given set.

• Loop through i=1 to N.
• Add i to the result and make a recursive call to (N-i).
• Base case: when n becomes 0

See the code for better explanation and recursion tree.

CodeRun This Code

Run This Code

Output:
1111
112
121
13
211
22
31
4