Shortest Range in K-sorted Lists

Objective: You have k lists of sorted integers. Find the smallest range that includes at least one number from each of the k lists.

This is very nice and tricky solution, This problem was asked in the Google interview for software engineer position.

Example:

Shortest Range in K-sorted Lists – Example

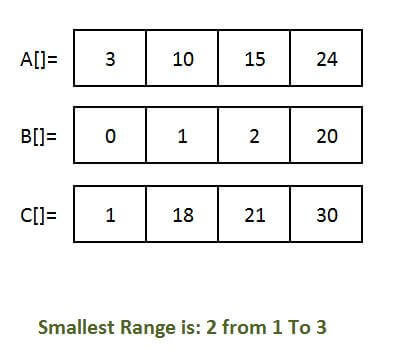
Smallest range will be 2, [1,3], it will contain 3 from list A[], 1 from list B[] and 2 from list C[].

Approach:

• We will modify the heap implementation for this solution. This approach will be quite similar to “Merge k-sorted array” solution we had discussed.
• Create Min-Heap of type HeapNode.( HeapNode- Every Node will store the data and the list no from which it belongs).
• Now take one element from each of the K list and create HeapNode object and insert into min-Heap.
• While inserting keep track of maximum value node inserted, call it as currMax.
• Extract the minimum Node from the min-Heap call it as min, calculate the range = currMax-min.
• The extracted node will also contain the list to which it belongs, insert the next element from that list into min-Heap.
• Keep track of the minimum range after every iteration of extracting min node and inserting new node into the heap.
• If any point of time any list gets over, return the range, this will be the smallest range in K-list which contains at least one element from each list.
• See the gif below for better understanding.

Shortest Range in K-sorted Lists

Complete Code:Run This Code

Run This Code
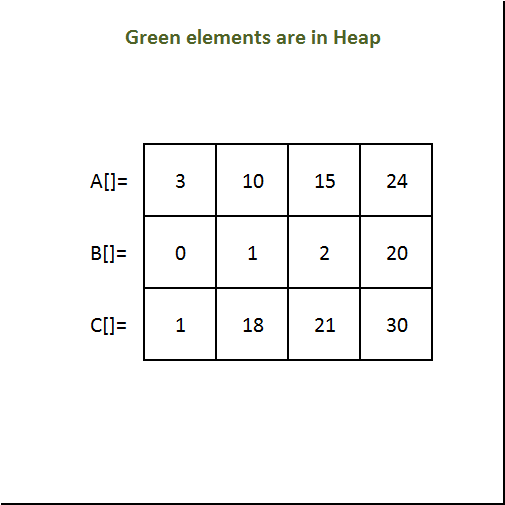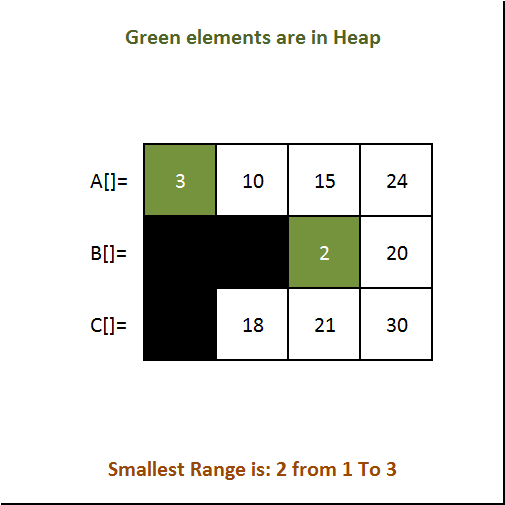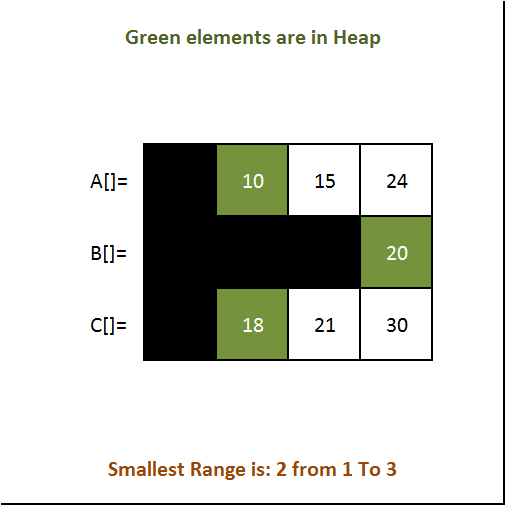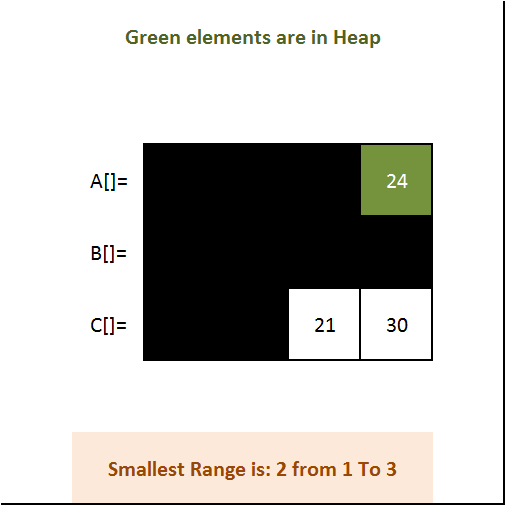
Output:

Smallest Range is: 2 from 1 To 3