|
Be the first user to complete this post
|
Add to List |
379. Sieve of Eratosthenes - Find all Prime Numbers less than equal to N | Set 2
Objective: Given a number N, Write a program to find all prime numbers which are between 0 and N using Sieve of Eratosthenes algorithm.
Prime Number: A prime number is a natural number that has exactly two distinct natural number divisors: 1 and itself.
Example:
N = 10 Output: 2 3 5 7 N = 60 Output: 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59
Earlier we had discussed O(N Sqrt(N)) solution - Find all Prime Numbers less than equal to N | Set 1. In this post we will discuss the Sieve of Eratosthenes algorithm to do the same, this algorithm works better than the approach we had discussed earlier.
Sieve of Eratosthenes Algorithm:
To find all the prime numbers less than or equal to a given integer n by Eratosthenes' method:
- Create a binary array of size N, let's say it prime[]
- Put 1 at all the indexes of the array, prime[].
- Iterate p = 2 to N (Will start from 2, smallest prime number).
- check if prime[p] =1, if yes then p is a prime number.
- Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the array as prime[2p]=0, prime[3p]=0 and so on (these will be 2p, 3p, 4p, ...; the p itself should not be marked).
- do the above two steps for all the p from 2 to N
- When the algorithm terminates, the indexes in the array prime[] for which the values are 1, are all the primes below N.
See the walkthrough as an example for more understanding.
N = 60, create an array prime[] from 1 to 60 and put 1. (Color all white)
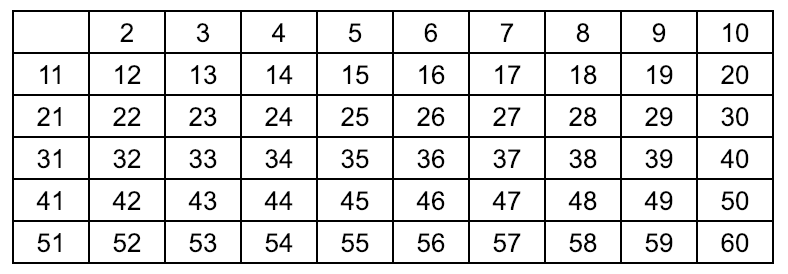
Find the first number in an array which is white (means prime[p]=1), found p = 2
Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the array as prime[2p]=0, prime[3p]=0 (color these green), 2 is a prime number (color it pink)
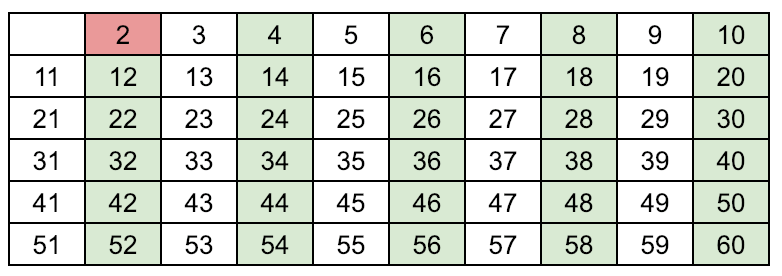
Find the next number in the array which is white, (means prime[p]=1), found p = 3
Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the array as prime[2p]=0, prime[3p]=0 (color these green), 3 is a prime number (color it pink)
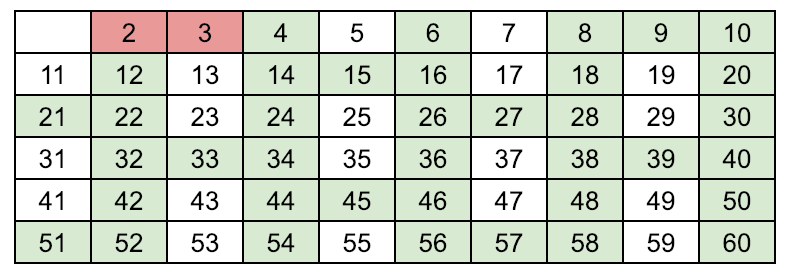
Find the next number in the array which is white, (means prime[p]=1), found p = 5
Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the array as prime[2p]=0, prime[3p]=0 (color these green), 5 is a prime number (color it pink)
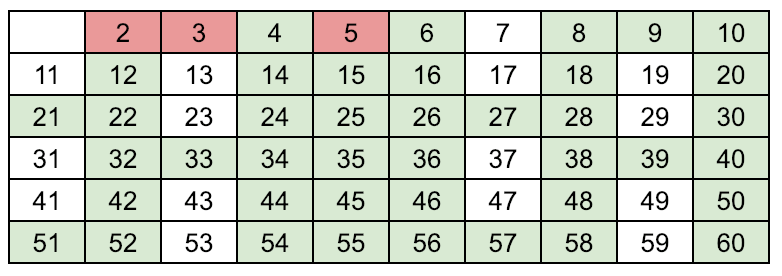
Find the next number in the array which is white, (means prime[p]=1), found p = 7
Enumerate the multiples of p by counting in increments of p from 2p to n, and mark them in the array as prime[2p]=0, prime[3p]=0 (color these green), 7 is a prime number (color it pink)
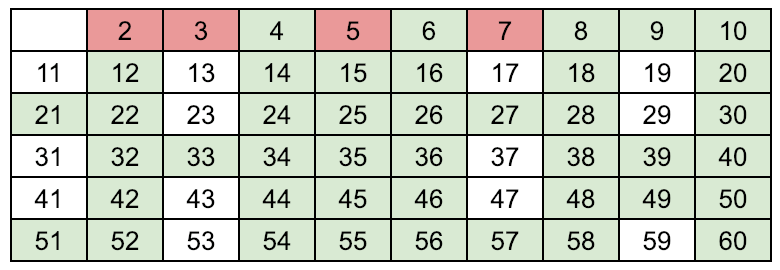
When the algorithm terminates, the indexes in the array prime[] for which the values are 1(pink color), are all the primes below N
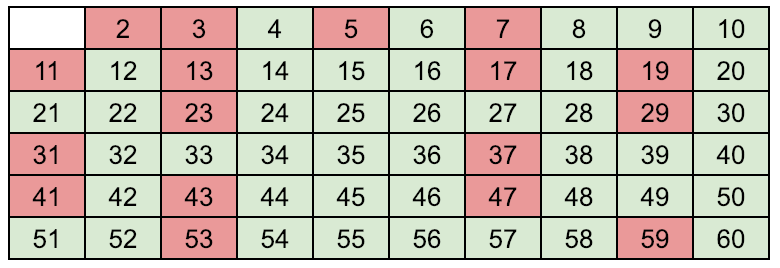
Output:
Number of Prime numbers less than N=60
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59
Reference: Wiki, geeksforgeeks

