|
This post is completed by 2 users
|
Add to List |
271. Snake and Ladder Problem
Objective - Given a snake and ladder game, write a function that returns the minimum number of jumps to take top or destination position.
You can assume the dice you throw results in always favor of you means you can control the dice.
Rules:
- Start from cell 1.
- Throw the dice and whatever number you get, move on the number of cells on the board.
- If you reach a cell which is base of a ladder, then you have to climb up that ladder without a dice throw.
- If you reach a cell is mouth of the snake, has to go down to the tail of snake without a dice throw.
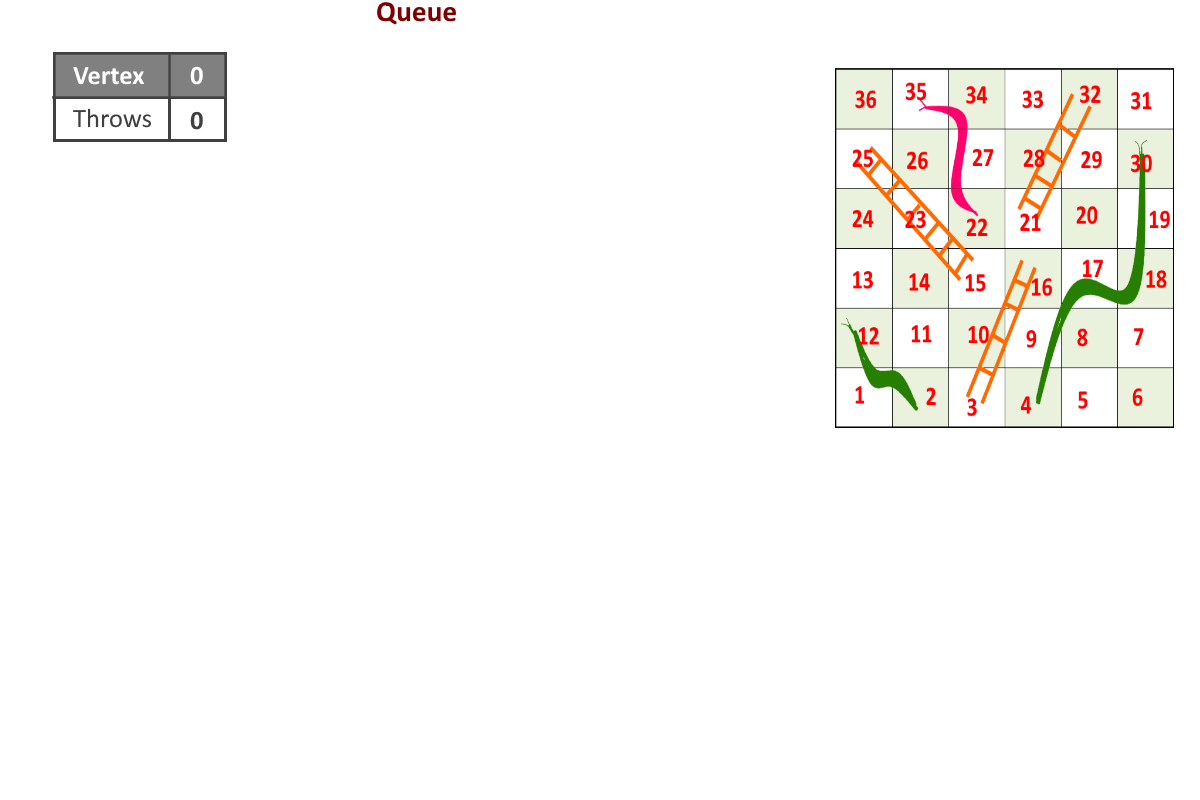
Example:
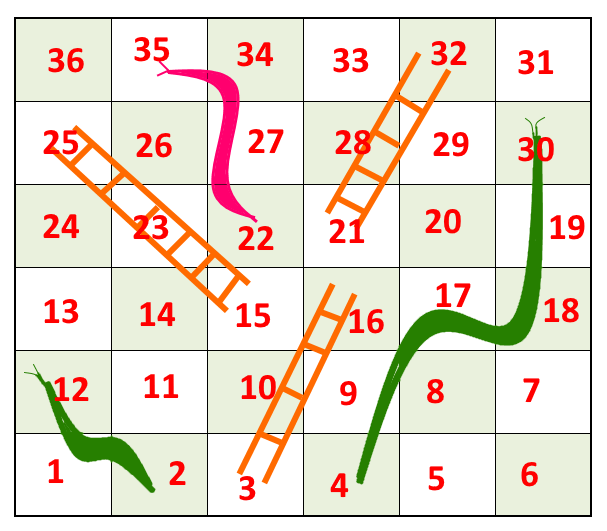
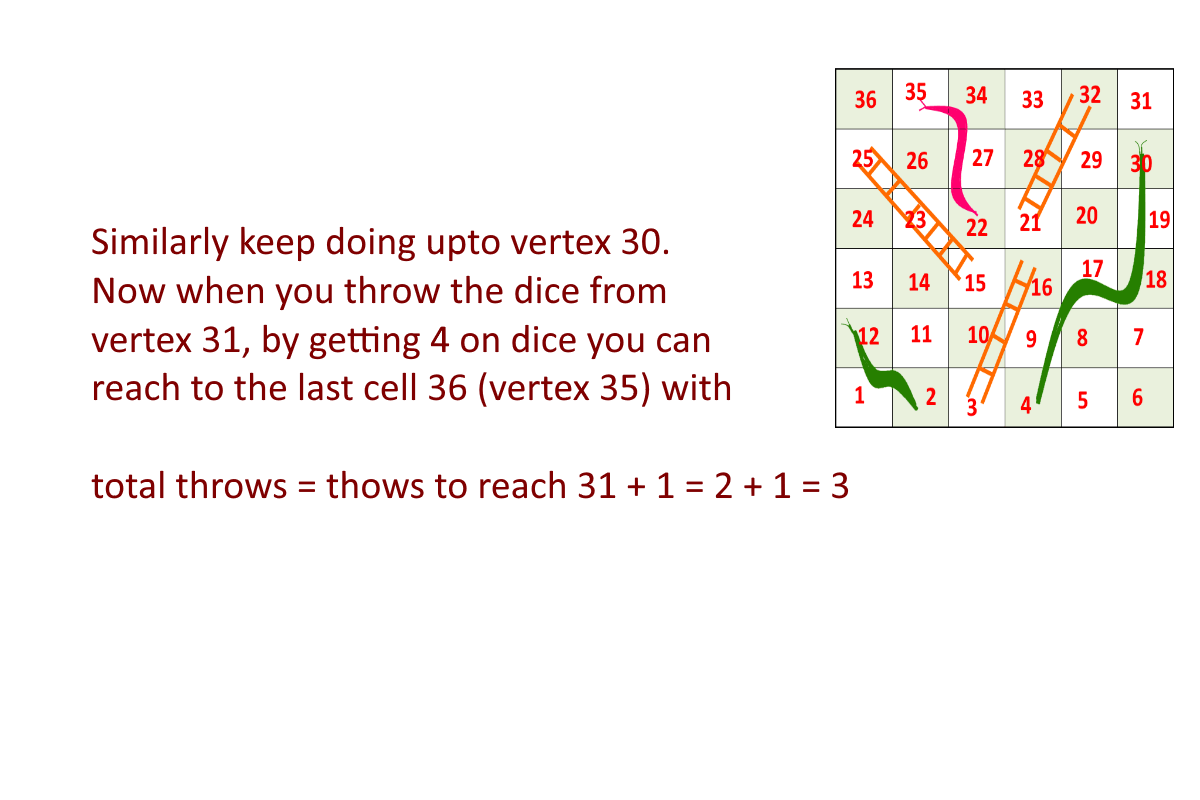
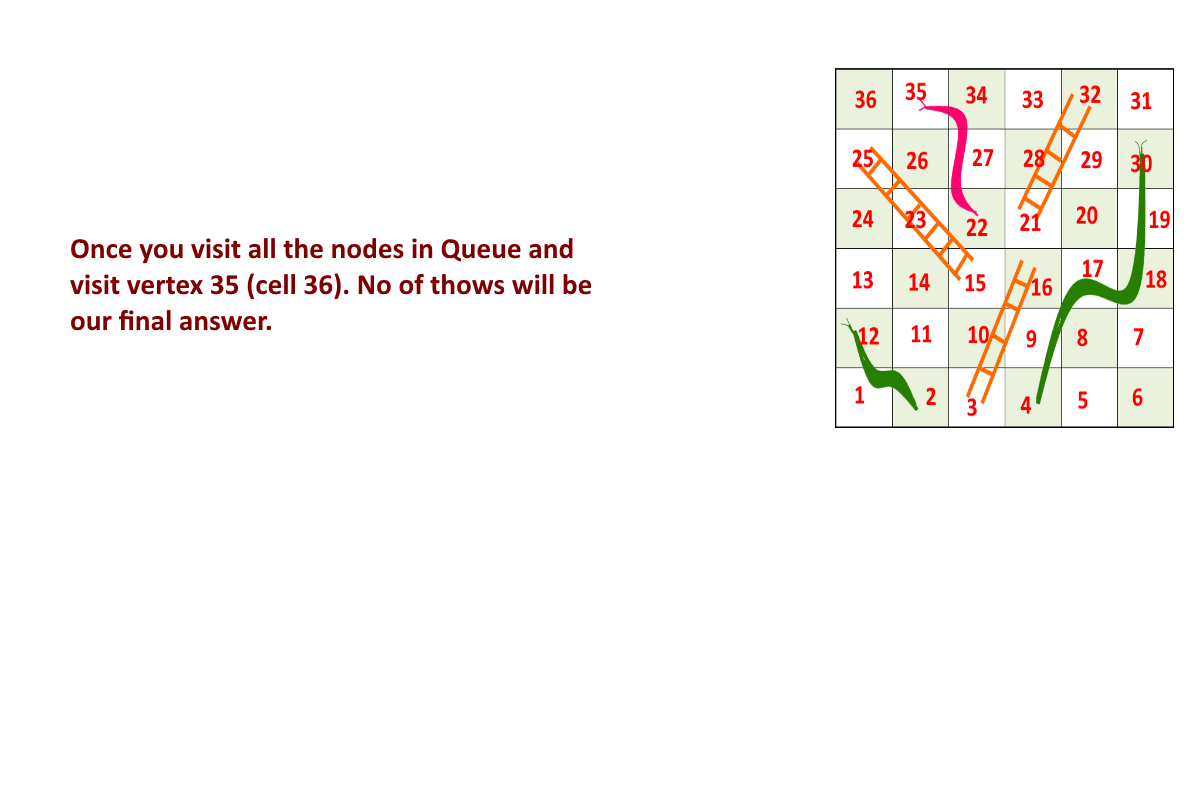
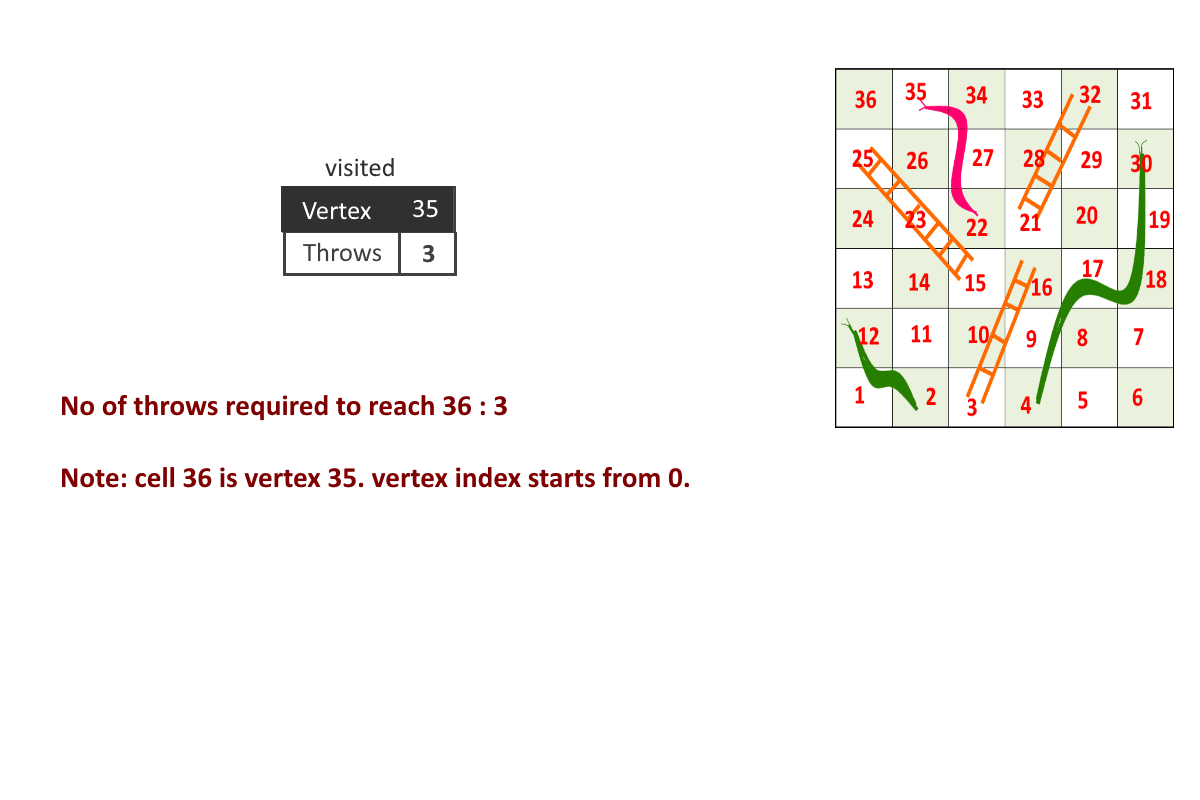
Minimum moves required to reach end (36th cell) from start(1st cell) = 3
- First throw on dice, get 2 to reach cell number 3, then take the ladder to reach 16.
- Second throw on dice to get 5 to cell number 21, and then take ladder to reach 32.
- Third throw on dice to get 4 to reach cell number 36.
Approach:
- Consider each as a vertex in directed graph.
- From cell 1 you can go to cells 2, 3, 4, 5, 6, 7 so vertex 1 will have directed edge towards vertex 2, vertex 3….vertex 7. Similarly consider this for rest of the cells.
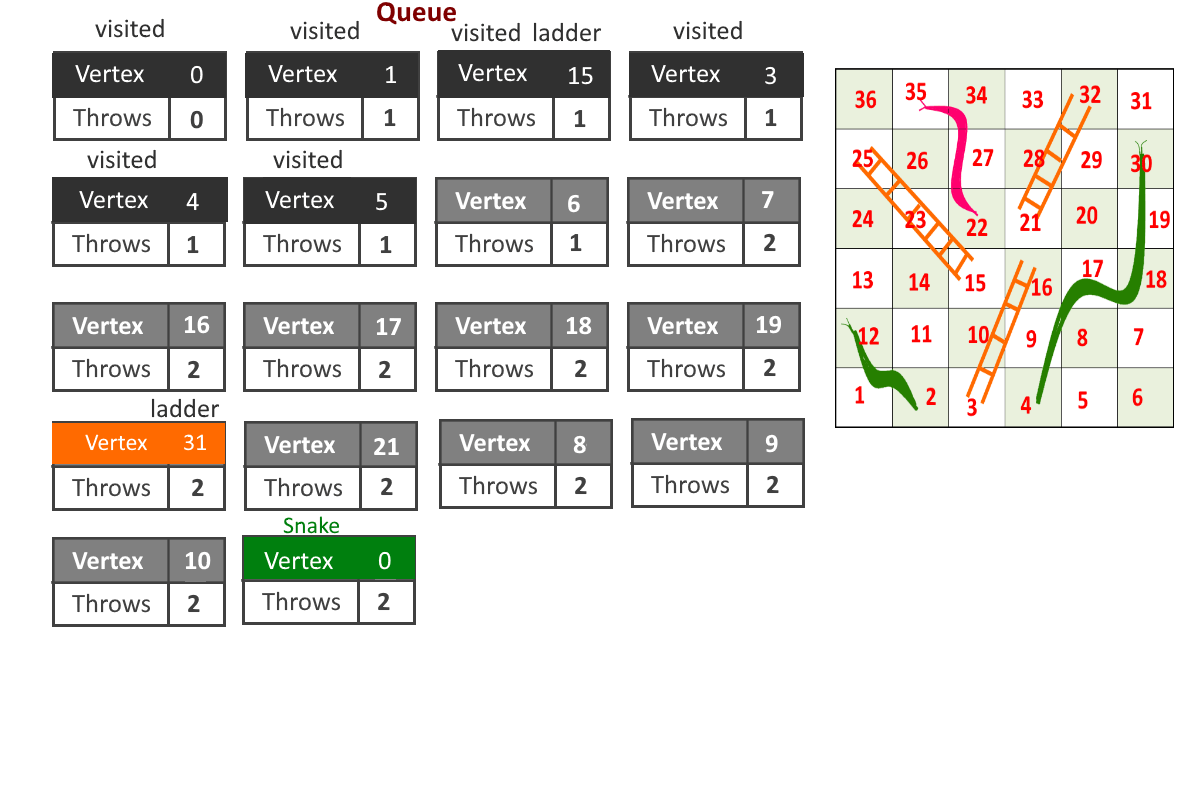
- For snake- connect directed edge from head of snake vertex to tail of snake vertex. (See example image above- snake from 12 to 2. So directed edge from vertex 12 to vertex 2)
- For ladder- connect directed edge from bottom of ladder vertex to top of the ladder vertex.
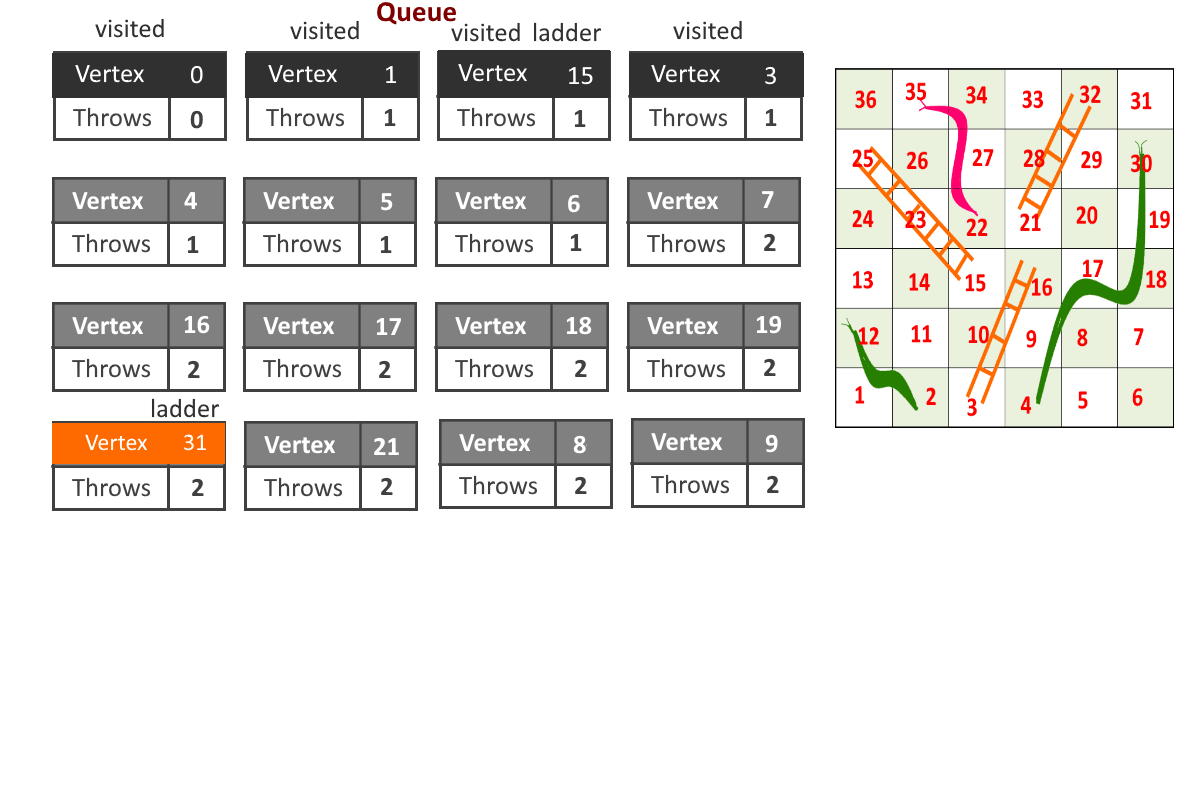
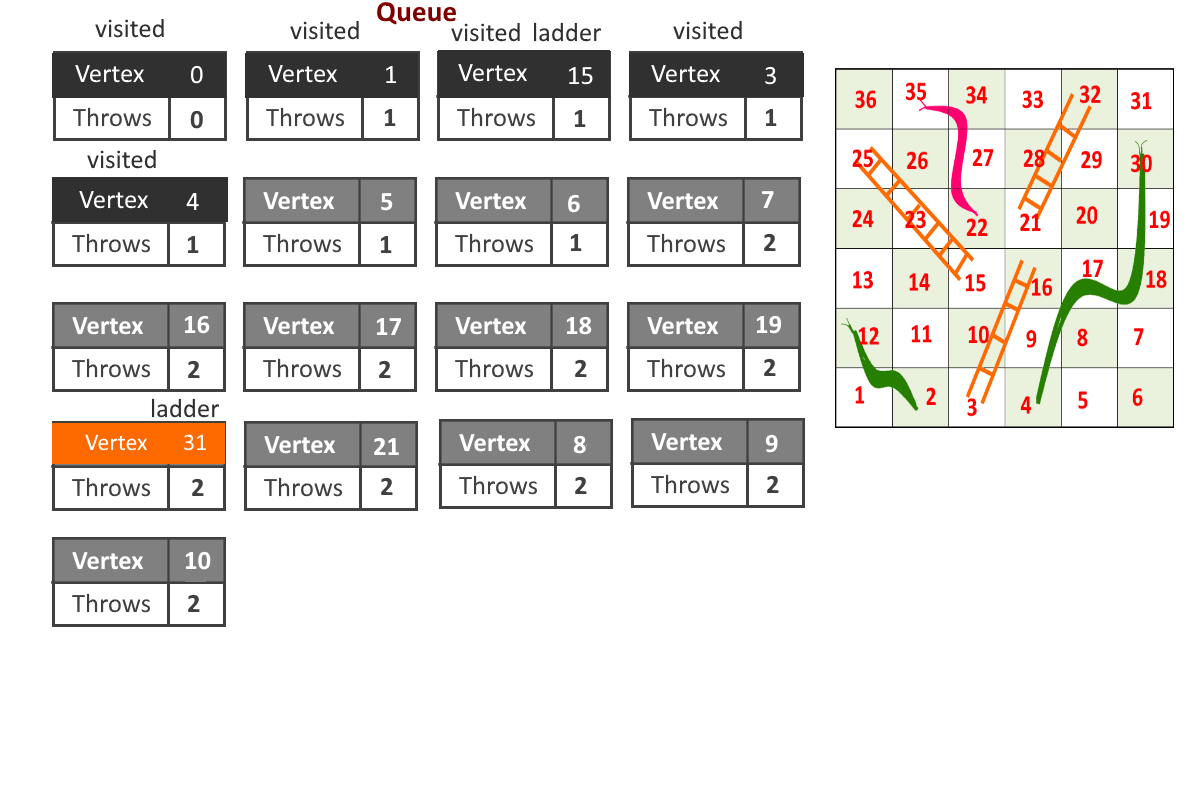
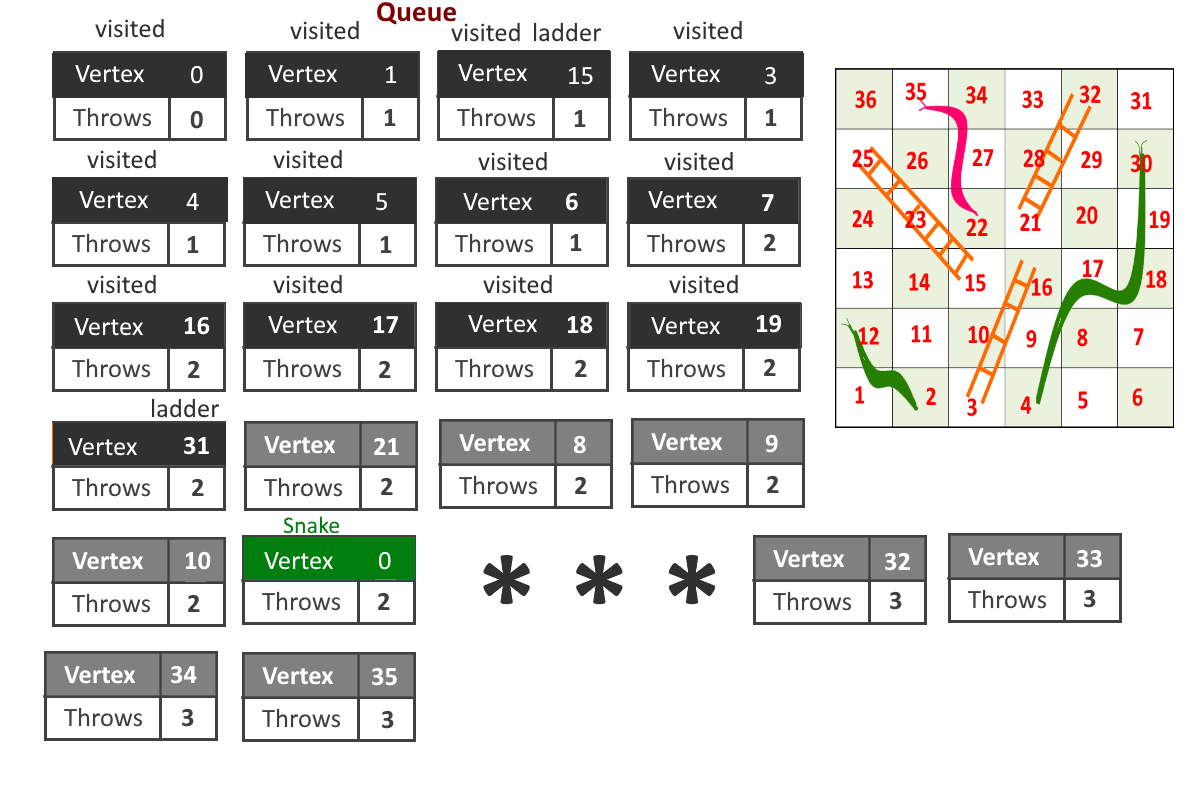
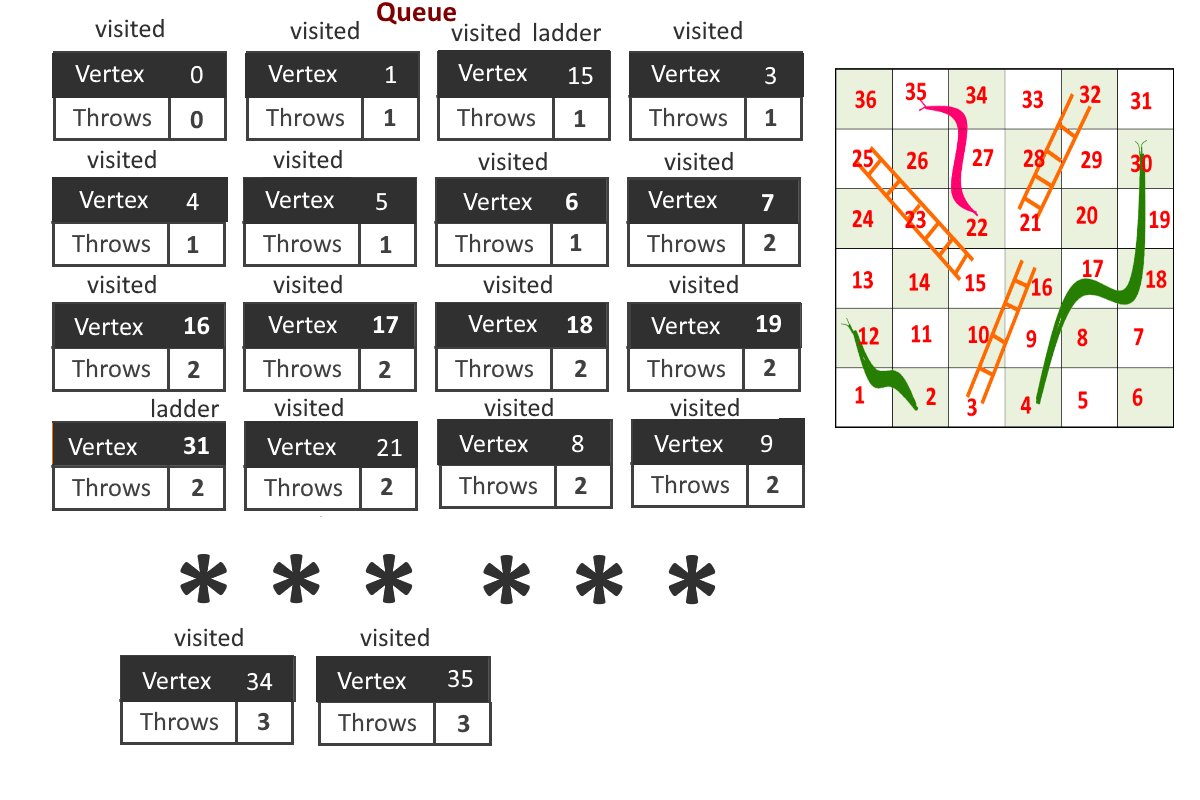
- Now problem is reduced to Shorted path problem. So by Breadth-First Search (using queue) we can solve the problem.
Implementation:
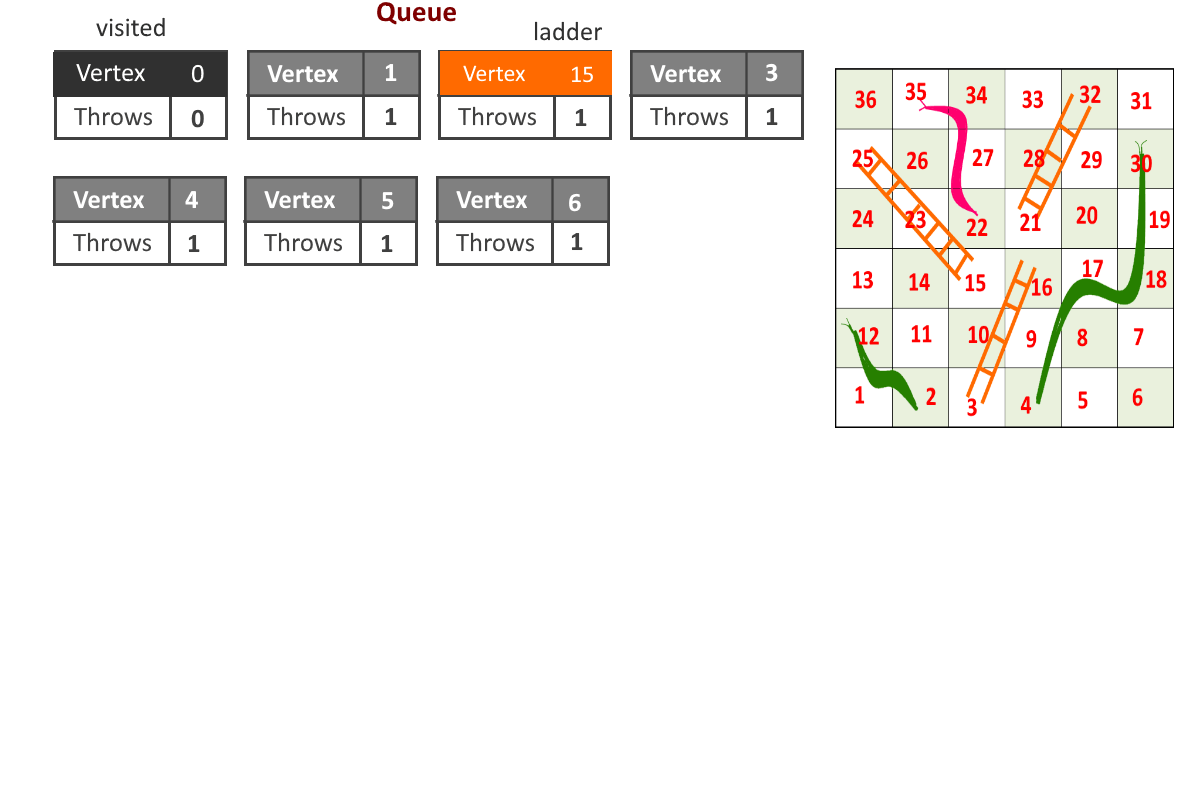
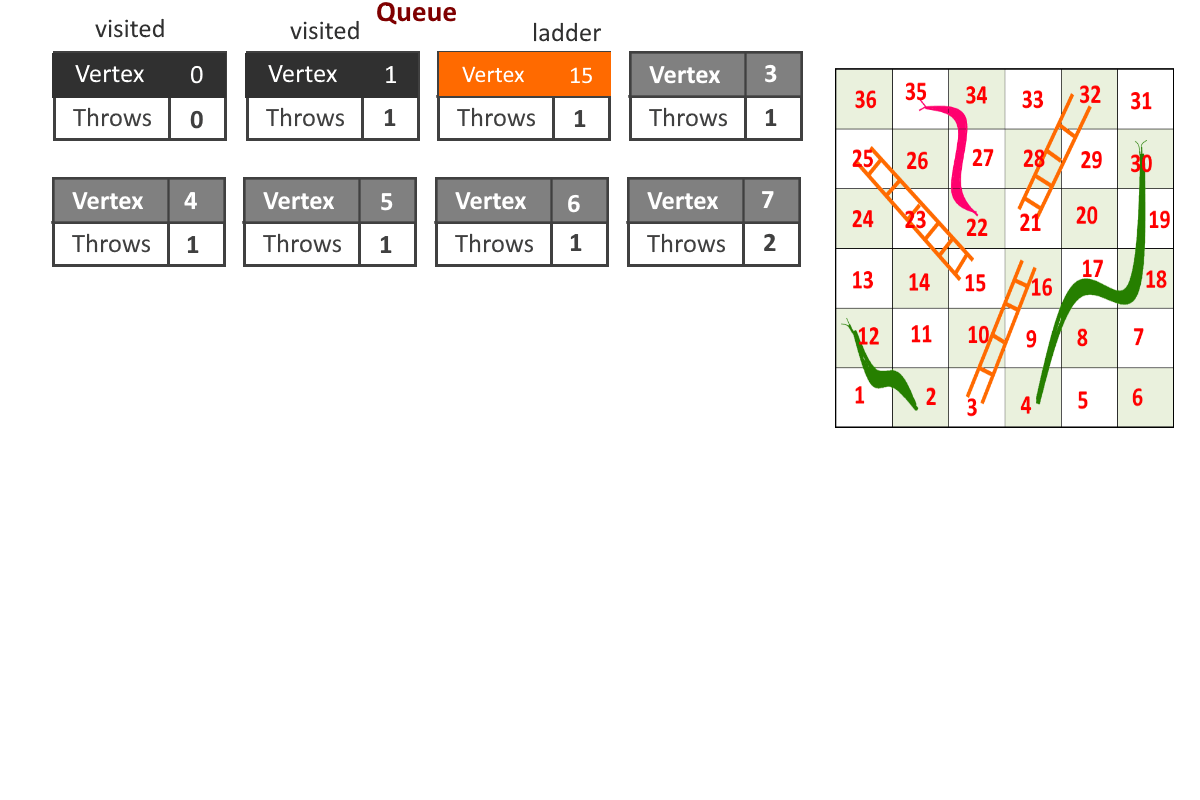
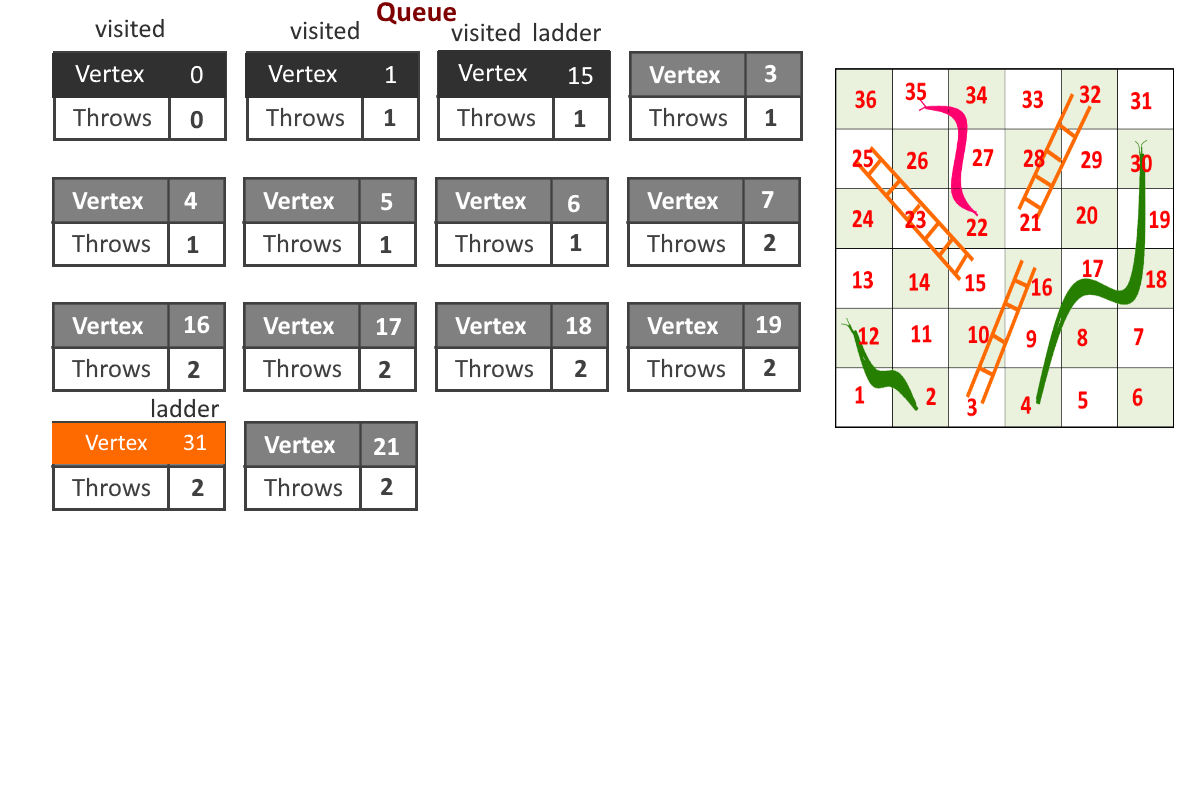
- Each vertex will store 2 information, cell number and number of moves required to reach to that cell. (cell, moves)
- Start from cell (vertex) 1, add it to the queue.
- For any index = i, Remove vertex ‘i’ from queue and add all the vertices to which can be reached from vertex ‘i’ by throwing the dice once and update the moves for each vertex (moves = moves to reach cell ‘i’ + 1 if no snake or ladder is present else moves = cell to which snake or ladder will leads to)
- Remove a vertex from queue and follow the previous step.
- Maintain visited[] array to avoid going in loops.
- Once reach to the end(destination vertex), stop.
See the animation below for more understanding.
Time Complexity: O(N)
Output:
Minimum Dice throws needed to reach to end: 3
Reference: here