Towers Of Hanoi

The Tower of Hanoi is a mathematical game or puzzle. It consists of three rods, and a number of disks of different sizes which can slide onto any rod.

The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:

1. Only one disk is allowed to move at a time..
2. Bigger disk cannot be placed on the top of smaller disk.

Tower-Of-Hanoi

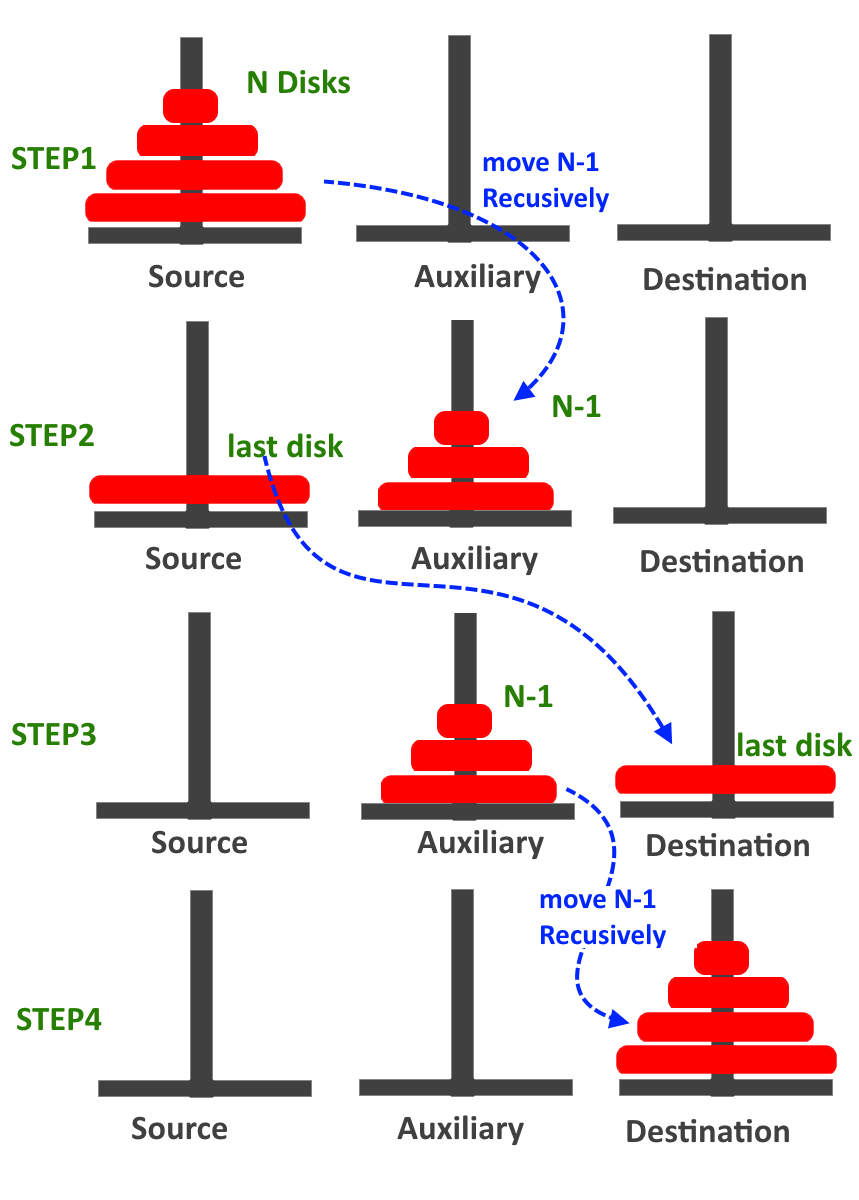
Approach:

• Recursively Move N-1 disk from source to Auxiliary peg.
• Move the last disk from source to destination.
• Recursively Move N-1 disk from Auxiliary to destination peg.

Code:Run This Code

Run This Code
Output:

Move disc 1 from A to C
Move disc 2 from A to B
Move disc 1 from C to B
Move disc 3 from A to C
Move disc 1 from B to A
Move disc 2 from B to C
Move disc 1 from A to C
Move disc 4 from A to B
Move disc 1 from C to B
Move disc 2 from C to A
Move disc 1 from B to A
Move disc 3 from C to B
Move disc 1 from A to C
Move disc 2 from A to B
Move disc 1 from C to B